Лекция 7

R
Автор

Е. Тымченко

Дата публикации

15 августа 2023 г.

Повторение

В этом курсе мы прошли большой путь. Мы поставили цель - найти связи между явлениями из действительности. Найти эти связи, а также проанализировать то, насколько точно мы их определили, нам помогла главная идея курса - оценка линейной модели при помощи метода наименьших квадратов. Наиболее лаконичное и просто лучшее резюме по этой теме можно посмотреть здесь.

Мы выяснили, что метод наименьших квадратов позволяет получить лучшие оценки интересующих нас параметров, если выполнены несколько условий из теоремы Гаусса-Маркова.

Gauss-Markov

Последнее условие не относится напрямую к ТГМ, но статистические тесты о значимости коэффициентов и значимости модели предполагают, что это свойство выполнено, поэтому важно о нём помнить.

Если все условия ТГМ выполнены - мы счастливы, потому что у нас уже есть лучшая из возможных оценок параметров. Тем не менее, на практике мы часто сталкиваемся с проблемой, когда часть условий не выполняется.

Источники проблем даже в простых линейных моделях могут быть разнообразными. Мы научились решать их, изучили:

Метод максимального правдоподобия

На идейном уровне он заметно отличается от метода наименьших квадратов и предполагает, что у нас, исследователей, есть вероятностная модель на основе которой мы описываем интересующее нас явление. Целевая функция здесь, функция правдоподобия - это вероятность обнаружить имеющиеся у нас данные при разных значениях параметров при условии, что наша вероятностная модель - верная.

Инструментальные переменные

Иногда мы сталкивались с тем, что влияние структура связей в моделируемом явлении достаточно сложна. Оценивать взаимосвязи в таких системах помогают инструментальные переменные - они не связаны напрямую с моделируемой переменной \(y\), но зато связаны с \(X\). Такими переменными, например, являлись налоги в модели потребления каких-либо товаров, когда налоги не влияют на решения о потреблении напрямую, зато значительно влияют на цены, а цены - на потребление. Моделирование таких связей важно для получения качественных результатов.

IV

Модели панельных данных

Мы также сталкивались с проблемой, когда наблюдения в нашей выборке не происходили из одной и той же генеральной совокупности. Например, экономический рост и продолжительность жизни для разных стран проистекают из совокупности факторов, характерных для этих стран. То есть, наблюдения в выборке - неоднородны, поскольку страны разные страны имеют довольно много характеристик, которые мы в модель не включаем, но которые играют в моделировании большую роль. Проблему неоднородности наблюдаемых стран/групп/индивидов помогает включение в модель фиксированных эффектов. Мы изложили указанную теорию и рассмотрели несколько примеров в лекции 6

Временные ряды

Временные ряды представляют собой последовательности случайный величин, упорядоченные по времени. Они - достаточно сложные объекты. Условия ТГМ для них выполняются редко, поскольку наблюдения \(x_t\) и \(x_{t-1}\) не независимы. Более того, такие наблюдения мы не можем разделить в независимые кластеры или группы. Для их анализа и прогнозирования разработаны специальные методы.

Пример 1

Бюджетное правило в России и связь нефтяных цен с валютным курсом.

Бюджетное правило в России имеет почти 20-летнюю историю, истоком которой является создание Стабилизационного фонда в 2004 году. Идея была в расширении возможностей фискальной власти в проведении контрциклической политики. Если цена нефти превышала базовую (20$ в 2004-2005гг. и 27$ с 2006 г.), то дополнительные доходы бюджета от экспортной пошлины на нефть и от НДПИ направлялись в Стабфонд. Это позволило сбалансировать расходы бюджета во времени.

Данное правило с течением времени менялось. В 2008 году Стабилизационный фонд был разделён на 2:

  • Фонд национального благосостояния, целью которого было обеспечение стабильности расходов бюджета,
  • Фонд национального благосостояния, целью которого было пенсионное обеспечение граждан.

Из-за кризиса 2007-2009 года данное правило было приостановлено в 2009-2012 г., а в 2013 году вышла его новая, весьма неудачная версия, где цена отсечения была зависима от нефтяных котировок. При этом, сама идея, из-за которой фискальное правило было введено, куда-то улетучилась и этот период эквивалентен отсутствию бюджетного правила.

В 2017 году введено бюджетное правило, которое не зависело от цены на нефть. Цена отсечения устанавливалась на уровне 40$ с ежегодно индексацией на 2% (предполагаемый уровень инфляции в развитых странах). Мы предполагаем, что именно эта версия бюджетного правила позволила значительно снизить влияние нефтяных цен на валютный курс.

Пока что мы ничего не знаем о временных рядах, но хотим проверить гипотезу о том, что до 2017 г. влияние нефтяных цен на валютный курс было большим, а с введением бюджетного правила 2017 г. оно стало меньше. прежде чем строить регрессионную модель, взглянем на данные:

нам понадобятся библиотеки

library(tidyverse) # обработка данных
library(aTSA) # статистические тесты
library(showtext) # рендер текста
library(sysfonts) # шрифты
library(rcartocolor) # работа с цветом
library(reshape2) # Обработка данных
library(stargazer) # таблички с результатами моделей
library(patchwork) # Комбинирование графиков
library(gganimate) # Анимации
showtext.auto()

Добавляем шрифт:

font_add(family = 'HSESans', regular = "\\HSESans-Bold.otf")

Загрузка макроэкономических радов для России

data <- read.csv('https://raw.githubusercontent.com/ETymch/Econometrics_2023/main/Datasets/econ_macro_data.csv') %>%
  select(-X) %>%
  mutate(Date = as.Date(Date))

Нарисуем зависимость валютного курса от нефтяных цен для двух периодов: 2011-2016 и 2017-2022 гг:

data %>%
  select(Date, USD, Urals) %>% # Выбираем интересующие нас ряды
  mutate(budget_rule = ifelse(Date <= '2017-01-01', 'До 2017 г.', 'После 2017 г.')) %>% # Создаём переменную-индикатор для периода после 2017г.
  ggplot(aes(x = as.numeric(Urals), y = as.numeric(USD), group = budget_rule)) + # по оси x - Urals, по оси y - валютный курс, групппировка - по периодам
  geom_point(aes(color = budget_rule), size = 3, show.legend = F, alpha = 0.5) + # точки с цветом, в зависимости от периода
  scale_color_carto_d(palette = 'Fall') + # Цвета точек из палитры Fall
  facet_wrap(~budget_rule) + # разбиение на 2 графика в зависимости от значений переменной `budget rule`
  theme_minimal(base_family = 'HSESans', base_size = 13) + # Тема, шрифт, размер шрифта
  labs(x = 'Цены на нефть', y = 'Курс доллара') # подписи осей

Budget Rules

Тепер оценим регрессионную модель:

\[USD_t = \alpha + \beta Urals_t + \varepsilon_t\] для трёх периодов:

  • Весь временной интервал: 2011-2022 гг.
  • Отсутствие де-факто бюджетного правила: 2011-2016 гг.
  • Наличие бюджетного правила: 2017-2022 гг.
data_1 <- data %>%
  filter(Date < '2017-01-01') # данные за 2011-2016 гг.
data_2 <- data %>%
  filter(Date >= '2017-01-01') # данные за 2017-2022 гг.

model <- lm(USD ~ Urals, data) # модель для всей выборки
model_1 <- lm(USD ~ Urals, data_1) # модель для выборки с 2011 по 2016 гг.
model_2 <- lm(USD ~ Urals, data_2) # модель для выборки с 2017 по 2022 гг.

stargazer(model, model_1, model_2, type = 'html', header = F) # сравнение моделей
Dependent variable:
USD
(1) (2) (3)
Urals -0.520*** -0.505*** 0.041
(0.033) (0.014) (0.068)
Constant 93.545*** 86.451*** 64.283***
(2.599) (1.262) (4.372)
Observations 144 72 72
R2 0.636 0.950 0.005
Adjusted R2 0.634 0.949 -0.009
Residual Std. Error 10.482 (df = 142) 3.556 (df = 70) 8.480 (df = 70)
F Statistic 248.288*** (df = 1; 142) 1,323.305*** (df = 1; 70) 0.355 (df = 1; 70)
Note: p<0.1; p<0.05; p<0.01

Мы видим, что разница между результатами для 2 и 3 моделей существенна и бюджетное правило действительно изменило зависимость между курсом доллара и ценами на нефть.

Уточнение: для более строгого доказательства данной гипотезы нам нужно придумать альтернативные объяснения исчезновению данной зависимости и статистически их отвергнуть.

Но как эти модели помогут нам прогнозировать? Какими статистическими свойствами они обладают? Давайте проанализируем, это даст нам понимание того, почему методы, которые мы применяли в начале курса, для временных рядов работают плохо.

# Сделаем функцию для графиков

make_ggdensity <- function(resid, tit, col, col1){ # Аргументы: вектор с ошибками модели, название графика, цвет1, цвет2.
  resid %>% # берём вектор с ошибками модели
    as.tibble %>% # делаем из него табличку
    ggplot(aes(x = value)) + # делаем график, по оси х - ошибки
    geom_density(color = NA, fill = col, alpha = 0.8) + # построить функцию плотности, без заливки границы, заплонить цветом1, прозрачность - 0.8
    geom_vline(xintercept = mean(resid), color = col1, size = 1.1, linetype = 'dashed') + # добавить вертикальную линию со средним значением ошибки
    theme_minimal(base_family = 'HSESans') + # тема и шрифт
    theme(plot.title = element_text(hjust = 0.5)) + # название - по центру, а не сбоку
    labs(x = 'Ошибка', y = 'Функция плотности', # подписи осей и названия
         title = tit)
}

# Трижды используем нашу функцию:

p1 <- make_ggdensity(model$residuals, '2011-2022', '#CBF8DF', '#E5B9AD')
p2 <- make_ggdensity(model_1$residuals, '2011-2026', '#CBF8DF', '#E5B9AD')
p3 <- make_ggdensity(model_2$residuals, '2017-2022', '#CBF8DF', '#E5B9AD')

# Соединяем графики:

p1 | p2 |p3

error_densities

Как мы видим, ошибки в 1 и 3 моделях распределены не нормально. Этого можно было ожидать исходя из постановки нашего анализа. Для этих моделей мы не сможем выполнить статистические тесты стандартным образом. Ошибки в модели 2, наоборот, распределены нормально. Более того, \(R^2\) для данной модели составляет 0.95 - значит, что колебания нефтяных котировок объясняют 95% изменений валютного курса в этот период. Осталось только проверить - являются ли наши оценки лучшими из возможных. Проверим условия теоремы Гаусса-Маркова, а именно, условие:

\[E[\varepsilon_i |\varepsilon_j] = E[\varepsilon_i] = 0\]

plot_a <- best_model_residuals_auto <- 
  tibble(y = model_1$residuals,
    index = 1:length(model_1$residuals)) %>%
  ggplot(aes(x = index, y = y)) +
  geom_point(color = '#E5B9AD', alpha = 0.8, size = 3) +
  theme_minimal(base_family = 'HSESans') +
  theme(plot.title = element_text(hjust = 0.5)) +
  labs(y = 'Ошибки модели',
       x = 'Номер наблюдения',
       title = 'Ошибки в модели 2011-2016 гг.')

plot_b <- tibble(nd = rnorm(mean = 0, sd = 10, n = length(model_1$residuals)),
       index = 1:length(model_1$residuals)
       ) %>%
  ggplot(aes(x = index, y = nd)) +
  geom_point(color = '#E5B9AD', size = 3, alpha = 0.8) +
  theme_minimal(base_family = 'HSESans') +
  theme(plot.title = element_text(hjust = 0.5)) +
  labs(y = 'Ошибки модели',
       x = 'Номер наблюдения',
       title = 'Как выглядели бы ошибки без автокорреляции')

plot_a / plot_b

autocor_1

Автокорреляция ошибок - одна из основных проблем, с которыми мы сталкиваемся, когда работаем с временными рядами. Она проистекает из того, что наши наблюдения - не независимы. Мы можем в этом убедиться, проведя простой статистический тест. Для этого представим простую авторегрессионную модель AR(1):

\[y_t = \rho y_{t-1} + \varepsilon_t\] \[ \begin{align} \Delta y_t &= y_t - y_{t-1} \\ &= \rho y_{t-1} - y_{t-1} + \varepsilon_t \\ &= (\rho - 1) y_{t-1} + \varepsilon_t \\ &= \delta y_{t-1} + \varepsilon_t \end{align} \] В тесте Дики-Фуллера проверяется гипотеза, что \(\delta = 0\). Мы можем протестировать эту гипотезу в лоб, оценив параметр \(\rho\) в модели \(y_t = \rho y_{t-1} + \varepsilon_t\) и на основании предположения о нормальности, оценить вероятность (p-value) того, что \(\rho\) находится в каком-то \(\epsilon\)-интервале вокруг 1. Этим мы занимались в первой и второй лекциях курса.

model_1$residuals %>% adf.test(nlag = 1)
Augmented Dickey-Fuller Test 
alternative: stationary 
 
Type 1: no drift no trend 
     lag   ADF p.value
[1,]   0 -4.82    0.01
Type 2: with drift no trend 
     lag   ADF p.value
[1,]   0 -4.79    0.01
Type 3: with drift and trend 
     lag   ADF p.value
[1,]   0 -4.78    0.01
---- 
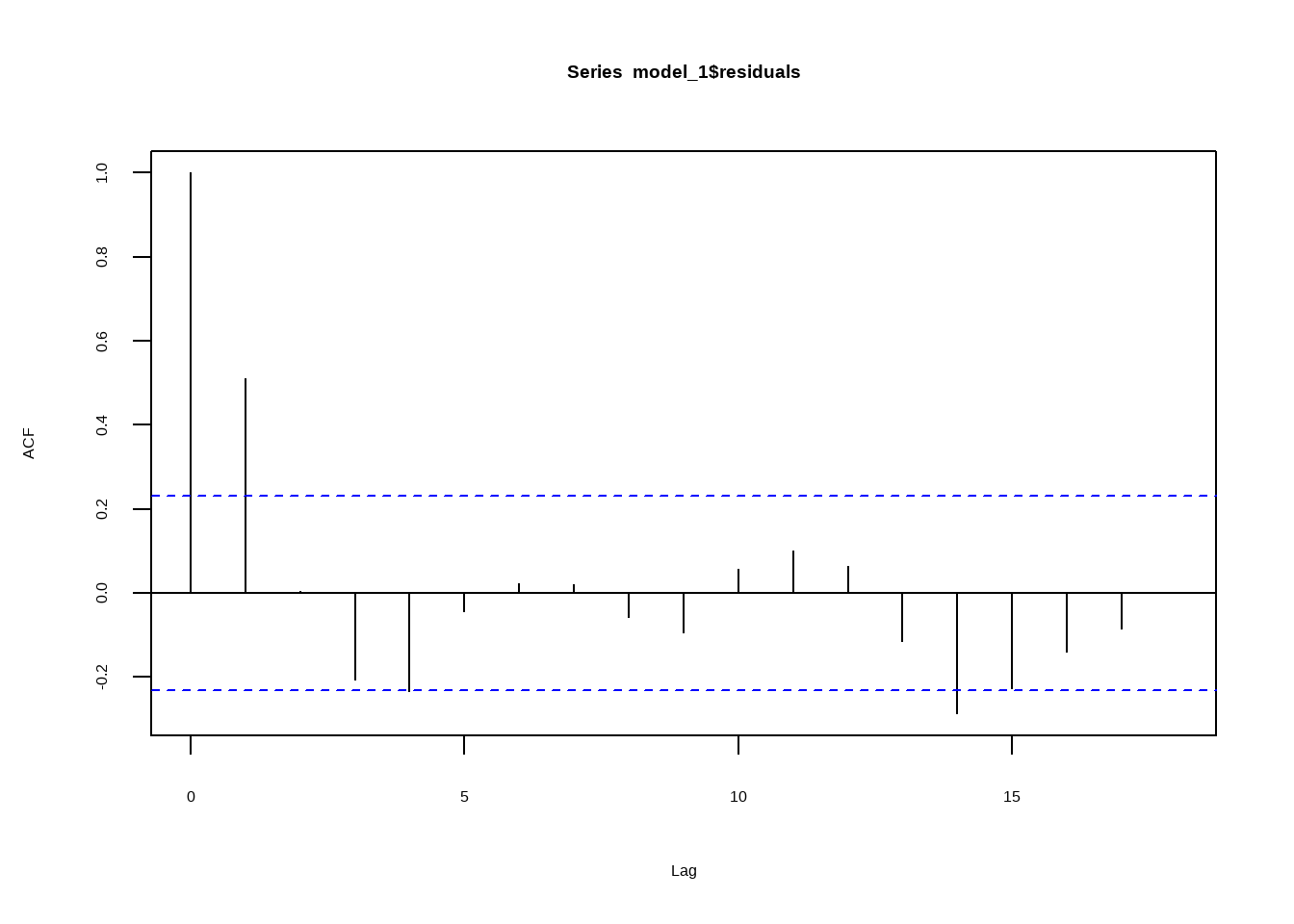
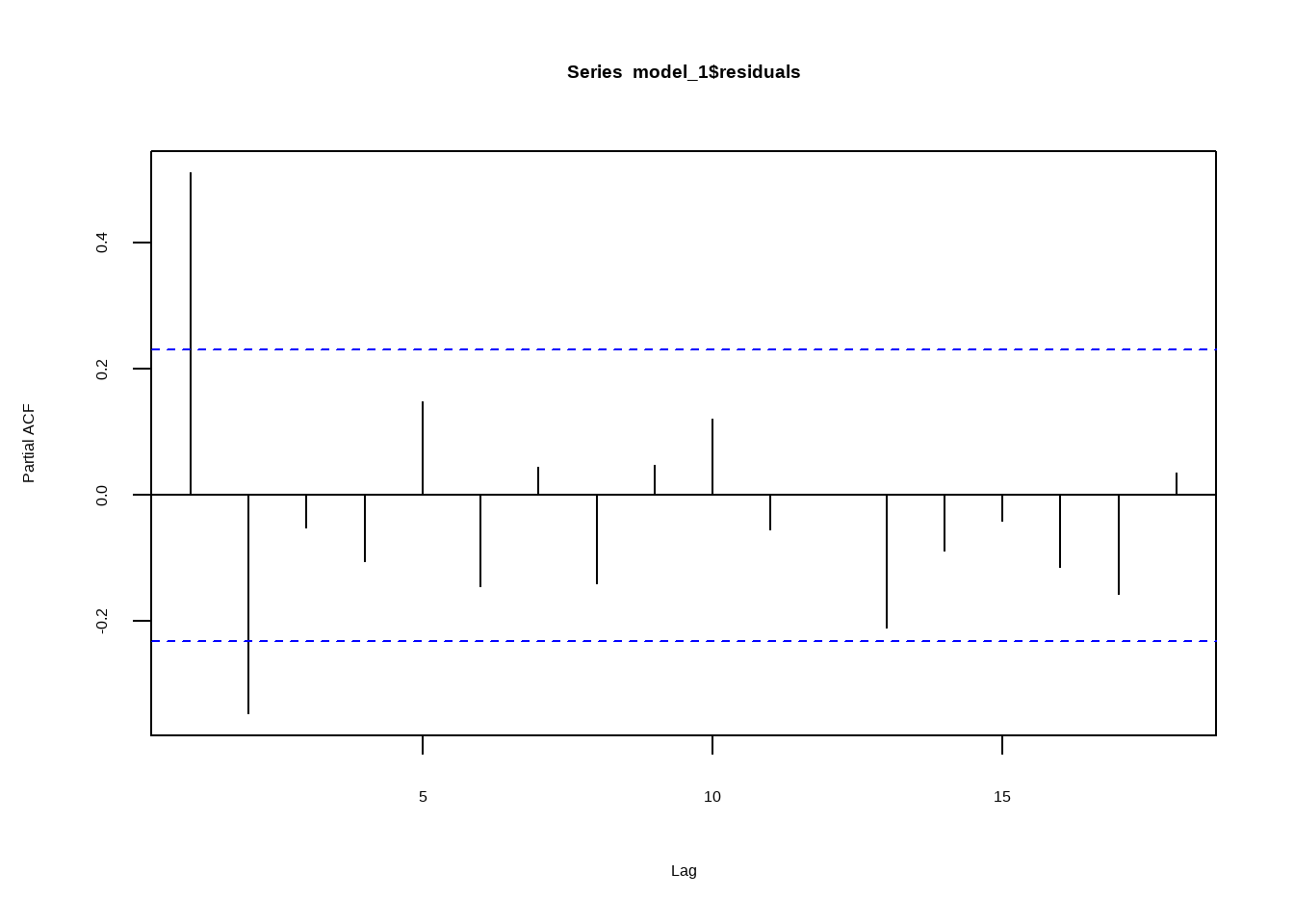
Note: in fact, p.value = 0.01 means p.value <= 0.01

Аналогичные результат мы можем получить, оценив параметр \(\rho\) для разных вариантов лага. Это можно сделать при помощи простой функции acf, встроенной в R.

acf(model_1$residuals)

Также существует родственная этой идея о том, что полезным бывает посмотреть на график частной автокорреляции. Частная автокорреляция временного ряда – это всего-навсего корреляция текущего наблюдения с прошлым.

pacf(model_1$residuals)

Если при попытках прогнозировать временные ряды, мы забываем о фундаментальной связи текущих исходов с прошлыми исходами, мы получаем систематические ошибки. Всё это мотивирует нас использовать иные методы при анализе временных рядов. Одной из важнейших концепций здесь служит идея о стационарности временного ряда:

Временной ряд считается стационарным (слабостационарным), если для него выполнены 2 условия: * На любых его промежутках среднее принимает одно и то же значение: \(\mathbb{E}x_i = \mathbb{E}x_j, \any i,j\) * На любых его промежутках, стандартное отклонение тоже является постоянной величиной.

например,

data %>%
  rename(c('Инфляция' = 'CPI',
           'Выпуск' = 'Output',
           'Ключевая ставка' = 'Key_Rate',
           'Ruonia' = 'Interbank_Rate')) %>%
  melt(id = 'Date') %>%
  ggplot(aes(x = Date, y = as.numeric(value), group = variable)) +
  geom_line() +
  scale_x_date(date_breaks = '3 years', date_labels = '%Y') +
  facet_wrap(~variable, scales = 'free') + 
  theme_bw(base_family = 'HSESans') +
  labs(x = 'Год', y = '')

macro ts

Мы видим, что ни один из макроэкономических временных рядов не может считаться стационарным. А значит, успешно прогнозировать их стандартными методами мы не сможем. Примечание: говоря с позиции практики, применение даже самых современных методов зачастую не приносит положительных результатов.

Как сделать временной ряд стационарным?

Временной ряд в общем виде можно разделить на три основных составляющих - тренд, сезонность и цикл. Тренд и сезонность - не позволяют ряду быть стационарным. Так, наличие тренда препятствует выполнению первого условия из определения стационарности, наличие сезонности - второго. Например, месячные данные о ВВП:

data$Output %>% # выбираем ВВП из таблички
  ts(start = c(2011,1), frequency = 12) %>% # Делаем временной ряд с месячной частотой `frequency = 12`.
  decompose() %>% # разложение на тренд, сезонность и цикл
  plot() # нарисовать

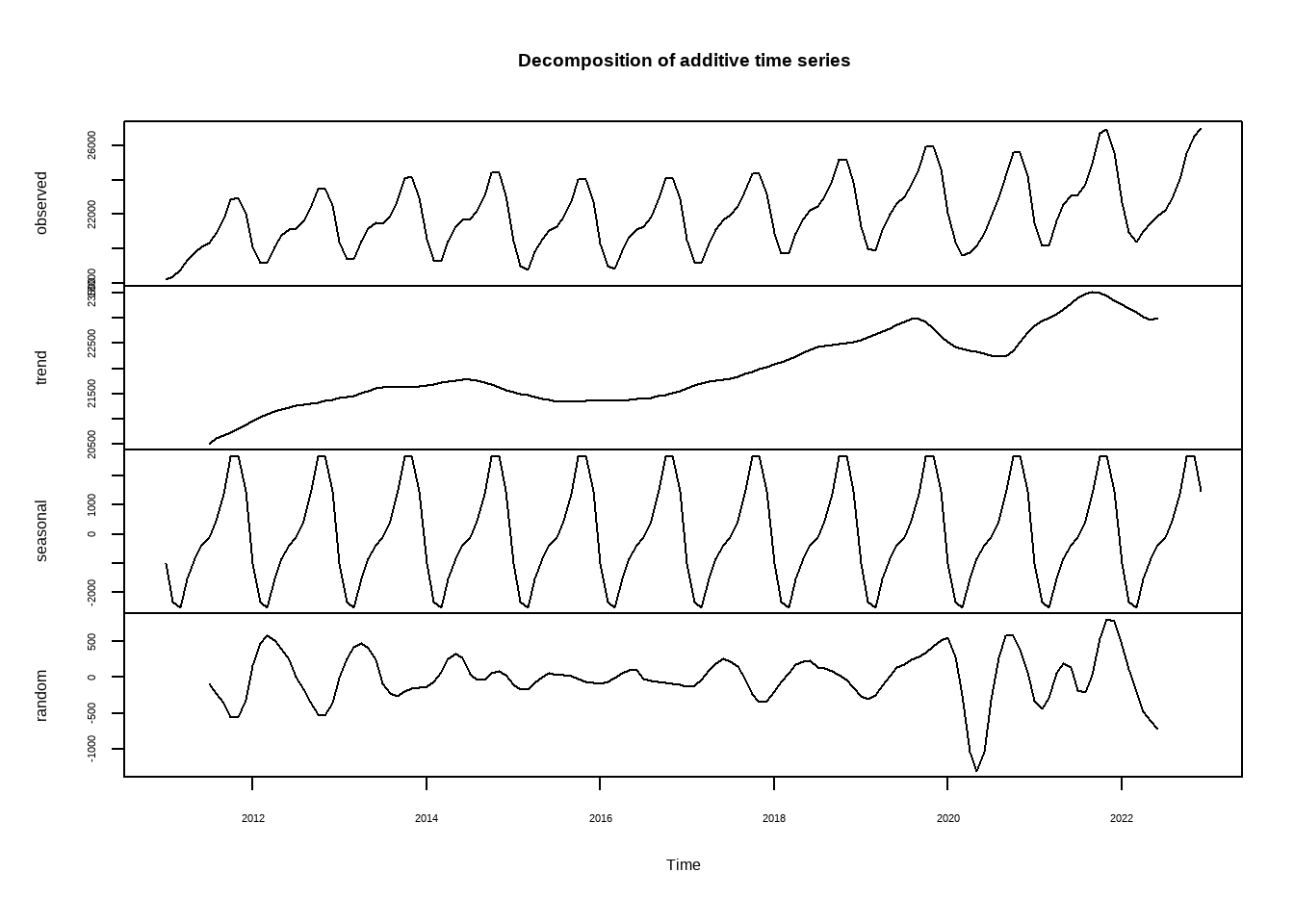
Функция decompose позволяет сделать простое разложение временного ряда \(y_t\) на три части: \(T_t, S_t, C_t\). Если эти части сложить, мы получим исходный ряд \(y_t\). Подробнее - в документации ?decompose.

\[ y_t = T_t + S_t + C_t \] В данном случае тренд определяется, как скользящее среднее (Moving average, MA порядка q):

\[ T_t = \phi_1(T_t - T_{t-1}) + \phi_2(T_{t-1} - T_{t-2}) + ... \] где q - количество параметров \(\phi\) в модели.

Сезонность в данном случае - всего-навсего среднее значение переменной в конкретный период.

Очистив ряд от тренда и сезонности мы остались один на один с компонентом временного ряда, представляющим для нас наибольший интерес - циклом:

y <- data$Urals %>%
  ts(start = c(2011,1), frequency = 12) %>%
  decompose()
y <- y$random %>% na.omit()

p1 <- y %>% pacf
p2 <- y %>% diff %>% pacf()

tibble(`Без дифференцирования` = p1$acf,
       `С дифференцированием` = p2$acf,
       lag = 1:length(p2$acf)
       ) %>%
  pivot_longer(cols = `Без дифференцирования`:`С дифференцированием`) %>%
  ggplot(aes(x = lag,
             y = value,
             color = name)) + 
  geom_point(alpha = 0.5, size = 3.5, show.legend = F) +
  geom_segment(aes(yend = 0, xend = lag), size = 2, alpha = 0.4, show.legend = F) +
  geom_hline(yintercept = -0.25, linetype = 'dashed', color = 'blue', alpha = 0.4) +
  geom_hline(yintercept = 0.25, linetype = 'dashed', color = 'blue', alpha = 0.4) +
  facet_wrap(~name, nrow = 2) +
  scale_color_carto_d(palette = 'Burg') +
  theme_minimal(base_family = 'HSESans') +
  labs(x = 'Лаг', y = 'PACF')

pacfs

Подведём итог:

  • Временные ряды состоят из трёх основных частей: тренд, сезонность, цикл. Эти части моделируются последовательно, сначала мы оцениваем тренд, потом сезонность, затем моделируем цикл.
  • Тренд и сезонность моделировать и прогнозировать проще, они меньше меняются с течением времени. Основные проблемы в прогнозировании временных рядов лежат в том, как нам лучше смоделировать цикл.
  • Циклическая компонента временного ряда обычно зависит от других временных рядов, имеет фундаментальное обоснование.

В заключительной части лекции рассмотрим то, как нам лучше моделировать тренд и сезонность.

Тренд

Рассмотрим различные варианты оценки тренда от простого к сложному:

Линейный тренд

Это самый простой, но вместе с тем, имеющий, как и все методы, свои ограничения, которые нам, как исследователям, нужно понимать. Для примера, оценим при помощи МНК простую модель:

\[ y_t = \beta_0 = \beta_1 t + \varepsilon_t \] Возьмём два временных ряда: выпуск и цена Urals. Как мы видели ранее, оба ряда - не стационарные. Значит, нам нужно найти способ выделить их тренд.

data <- data %>%
  mutate(t = 1:length(data$Date))

lt_output <- lm(Output ~ t, data)$fitted
lt_urals <- lm(Urals ~ t, data)$fitted

p1 <- tibble(output = data$Output,
       lt_output,
       date = data$Date
       ) %>%
  pivot_longer(output:lt_output) %>%
  ggplot(aes(x = date, y = value, color = name)) +
  geom_line(size = 2, alpha = 0.5, show.legend = F) +
  scale_color_carto_d(palette = 'TealRose', direction = -1) +
  theme_minimal(base_family = 'HSESans') +
  theme(plot.title = element_text(hjust = 0.5)) +
  labs(title = 'Выпуск', x = '', y = 'ВВП в ценах 2016 г., млрд. руб')

p2 <- tibble(urals = data$Urals,
       lt_urals,
       date = data$Date
) %>%
  pivot_longer(urals:lt_urals) %>%
  ggplot(aes(x = date, y = value, color = name)) +
  geom_line(size = 2, alpha = 0.5, show.legend = F) +
  scale_color_carto_d(palette = 'TealRose', direction = -1) +
  theme_minimal(base_family = 'HSESans') +
  theme(plot.title = element_text(hjust = 0.5)) +
  labs(title = 'Urals', x = '', y = 'Urals, долл. за барр.')

p1 / p2

linear_trends

Модели пространства состояний

Среди моделей, позволяющих отделить тренд от прочих составляющих временного ряда, наиболее удачными являются те, которые основаны на теории пространства состояний. Эта идея - одна из самых важных в анализе временных рядов, и мы уделим ей некоторое время. Своё первое значимое применение эти идеи получили в проекте Аполлон, когда модели пространства состояний, а именно, Фильтр Калмана, применялись для отследивания траекторий космических аппаратов. Сегодня улучшенные версии фильтра Калмана применяются в GPS, задачах беспилотного управления и многих других. В экономике модели пространства состояний, фильтры, применяются для декомпозиции временных рядов, а динамические стохастические модели общего равновесия [DSGE] оцениваются на данных в форме моделей пространства состояний.

В данный момент мы хотим выделить тренд временного ряда. Как о нём можно думать?

Когда мы работаем с временными рядами, то никаких трендов мы не наблюдаем. Мы наблюдаем конечные исходы, грязные данные, на которые влияет множество случайных событий, начиная от погрешностей при измерениях, заканчивая фундаментальным влиянием других переменных. Тренд здесь - спрятанное состояние - которое мы хотим определить. При этом, мы делаем упрощающее предположение:

  • Свойство Маркова - текущее состояние зависит только от состояния в прошлый момент времени. Иначе мы можем охарактеризовать это свойство, как короткая память.
  • наблюдение в текущий период зависит от текущего состояния.

state_space

Данную идею можно также изложить системой из двух уравнений. Пусть \(x_t\) - состояние системы в момент \(t\), \(y_t\) - наши наблюдения из таблички:

\[ x_t = f_x(x_{t-1}, \varepsilon_x) \\ y_t = f_y(x_{t}, \varepsilon_y) \] Для примера давайте ненадолго отвлечёмся от нашей задачки и получим больше интуиции относительно моделей пространства состояний. Рассмотрим простой пример, скрытую Марковскую модель - модель пространства состояний, в которой состояния - дискретные случайные величины. Это простой пример, в котором мы будем знать состояния, никаких параметров мы пока оценивать не будем. Куда важнее - выработать понимание того, как устроены марковские процессы.

Марковские модели выживания

Предположим, вы занимаетесь государственными программами обеспечения больных людей лекарствами. Вам нужно оценить ожидаемую величину трат на одного пациента при разных типах лечения, которая основана на стоимости самого лечения и ожидаемой продолжительности жизни при применении разных лекарств. Данный пример основан на статье в которой авторы выделяют 8 типов остеопороза и разные типы его лечения, оценивают параметры на данных и прогнозируют эффекты на продолжительность жизни пациентов и бюджет.

Для наччала, предположим, что состояний всего два:

  • “Здоровый”: \(\theta = 1\)
  • “Больной”: \(\theta = 2\)

Мы можем оценить из данных вероятности:

  • Вероятность того, что здоровый человек заболеет равна \(\alpha\).
  • Вероятность того, что больной человек выздоровеет, равна \(\beta\).

Данную структуру мы можем представить в виде матрицы:

\[ \begin{pmatrix} 0.95 & 0.05 \\ 0.6 & 0.4 \\ \end{pmatrix} \] в которой вероятность перехода из состояния \(i\) в состояние \(j\) - значение матрицы в ячейке \({ij}\). Заметьте, что сумма всех значений в каждой строке равна 1.

Зная эти вероятности, мы можем смоделировать динамику состояний для одного человека. Напишем функцию:

mc_path <- function(P, init, sample_size){

N = dim(P)[1] # Размерность матрицы

X = c() # Создадим пустой вектор
X[1] = init # Начальное состояние

for (t in 2:sample_size){
X[t] = sample(seq(1, N, by = 1), size = 1, prob = P[,X[t-1]]) # следующее значение
   }
 X
}

Проверим её:

alpha = 0.05 # Вероятность заболеть
beta = 0.6 # Вероятность выздороветь

P <-  matrix(c(1 - alpha,   alpha,
             beta,      1 - beta),
     nrow = 2)

X <-  mc_path(P, init = 1, sample_size = 50)
X
 [1] 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1
[39] 1 1 1 1 1 1 1 1 1 1 1 1

Мы можем узнать вероятность быть здоровым:

sum(X == 1)/length(X) # вероятность быть здоровым
[1] 0.96

Если мы запустим симуляцию для множества людей, то мы получим больше понимания, как устроен этот случайный процесс. Пока что мы учимся мыслить о марковских случайных процессах.

Давайте введём третье состояние - смерть так, что вероятность умереть больным - значительно выше вероятности умереть будучи здоровым.

# 3-е смерть.

alpha = 0.03 # вероятность заболеть
beta = 0.6 # вероятность выздороветь
gamma = 0.005 # вероятность умереть здоровым
delta = 0.02 # вероятность умереть больным

P = matrix(c(1 - alpha,    alpha-gamma,          gamma,
             beta,         1 - beta - delta,     delta,
             0,            0,                      1 ),
           nrow = 3
)

mc_path(P, 1, 100)
  [1] 1 1 1 1 1 2 1 1 1 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 [38] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 [75] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1

Проведём симуляцию для \(n\) человек:

n = 4
t = 400

Y = matrix(NA, nrow = t, ncol = n)
for (j in 1:n){
Y[,j] = mc_path(P, 1, sample_size = t)
}

Сделаем анимацию!

plot_animation <- 
  tibble(index = 1:t,
       first = Y[,1],
       second = Y[,2],
       third = Y[,3],
       fourth = Y[,4]
) %>%
  pivot_longer(cols = first:fourth) %>%
  ggplot(aes(x = name, y = value, color = name)) +
  geom_point(size = 4, alpha = 0.5, show.legend = F) + 
  scale_color_carto_d() +
  theme_minimal(base_family = 'HSESans', base_size = 22) +
  gganimate::transition_time(index) +
  labs(x = 'Период', y = 'Состояние')

animate(plot_animation, height = 6, width = 8, units = "in", res = 250, duration = 25,
        fps = 30, end_pause = 50, render = av_renderer("anim_mcmc.mp4"))