Лекция 6

R
Автор

Е. Тымченко

Дата публикации

25 июля 2023 г.

Панельные данные

Приводит ли рост цен на жильё к снижению динамики строительства? ответ на этот вопрос неочевиден. * С одной стороны, покупатели жилья видят увеличение цен, перестают покупать жильё -> у строителей меньше активов, строительство снижается. * С другой, очень часто может быть, что увеличение строительства - следствие увеличения спроса на жильё, а спрос в краткосрочном периоде сдерживается ценами. Как проверить, какой вариант выполняется?

Библиотеки:

library(tidyverse)
library(stargazer)
library(rio)
library(plm)
library(ggrepel)
library(sysfonts)
library(showtext)
showtext.auto()

font_add_google('Merriweather')
font_add_google('Lobster')
data_housing <- read.csv('https://raw.githubusercontent.com/ETymch/Econometrics_2023/main/Datasets/data.housing.csv') %>%
  tibble()

# Посмотрим на несколько наблюдений в начале таблицы:

data_housing %>%
  head()
# A tibble: 6 × 25
      X  ...1 Region      Date    NA. Population   HPI  S_Unf    HR   CPI GRP_pc
  <int> <int> <chr>       <chr> <int>      <dbl> <dbl>  <dbl> <dbl> <dbl>  <dbl>
1     1     1 Алтайский … 2002…     1   2624071.  129. 5.84e5 2143.  113. 27697.
2     2     2 Алтайский … 2002…     2   2622863.  127. 5.39e5 2143.  113. 27814.
3     3     3 Алтайский … 2002…     3   2620446.  123. 4.48e5 2142.  113. 28050.
4     4     4 Алтайский … 2002…     4   2616820.  118. 3.13e5 2141.  113. 28404.
5     5     5 Алтайский … 2003…     5   2611986.  111. 1.32e5 2139.  113. 28875.
6     6     6 Алтайский … 2003…     6   2606296.  106. 6.82e3 2139.  113. 29672.
# ℹ 14 more variables: HR_pc <dbl>, BP <dbl>, PI_Roads_Materials <dbl>,
#   Price_m2_fm <dbl>, Price_m2_sm <dbl>, Materials_pi <dbl>,
#   N_of_Credits <int>, Avg_IR <dbl>, Avg_Sum_of_credit <dbl>,
#   Avg_Duration_of_Credit <dbl>, Mortgage_Debt <dbl>, Usage <dbl>,
#   Usage_ratio <chr>, S_unf_redone <dbl>

Посмотрим, как выгляит строительство и стоимость жилья в статике:

data_housing %>%
  filter(Date == '2019-10-01', # Оставляем один период в выборке
         HPI <= 125) %>% # Убираем Москву, где индекс цен на жильё заметно выше, чем в других регионах.
  ggplot(aes(x = HPI, y = S_unf_redone, size = GRP_pc)) + # помимо осей х и у, размер кружочка - ВРП на душу населения.
  geom_point(alpha = 0.4, color = 'orange', fill = 'orange', show.legend = F) +
  geom_text_repel(aes(label = Region), size = 3, max.overlaps = 7 ,show.legend = F, family = 'Lobster',
                  nudge_x = 0.8, nudge_y = 100) + # Авоматические подписи
  theme_classic(base_family = 'Merriweather', base_size = 12) +
  scale_size_continuous(range = c(3, 15)) + # Минимальный и максимальный размеры кружочков
  labs(y = 'Площадь в процессе застройки, млн. м2', x = 'Индекс цен на недвижимость, г/г.', # Заголовки
       title = 'Стоимость недвижимости и динамика строительства',
       subtitle = '4 кв. 2019 г.',
       caption = '*Размер кружка - относительный ВРП на душу населения')
Warning: ggrepel: 42 unlabeled data points (too many overlaps). Consider
increasing max.overlaps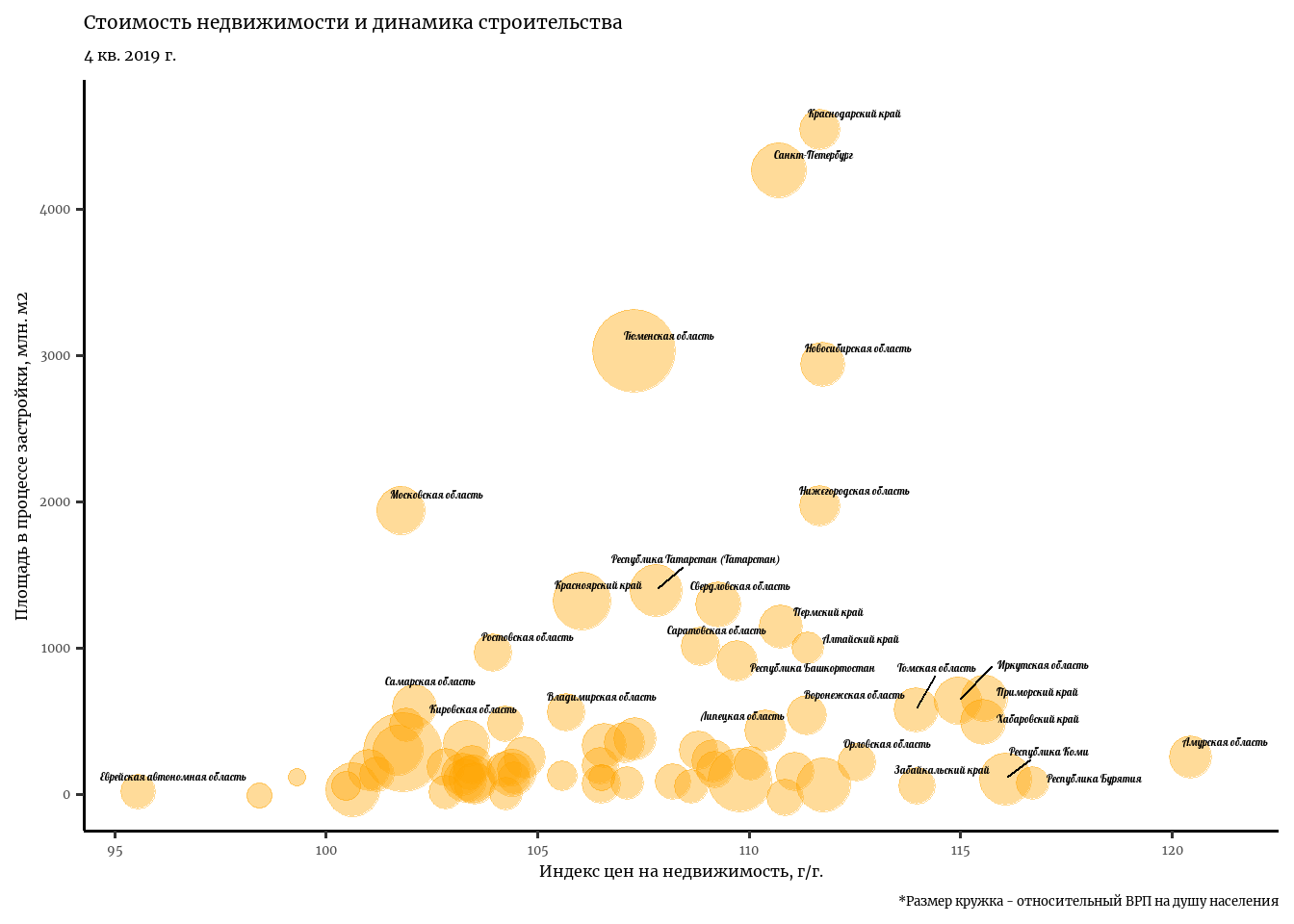

Мы хотим посмотреть, как изменялось это соотношение во времени. Сделать анимацию имея на руках готовый график - очень просто!

p <- data_housing %>%
  filter(HPI <= 125) %>% # Убираем Москву, где индекс цен на жильё заметно выше, чем в других регионах.
  ggplot(aes(x = HPI, y = S_unf_redone, size = GRP_pc)) + # помимо осей х и у, размер кружочка - ВРП на душу населения.
  geom_point(alpha = 0.4, color = 'orange', fill = 'orange', show.legend = F) +
  geom_text_repel(aes(label = Region), size = 4, max.overlaps = 7 ,show.legend = F, family = 'Lobster',
                  nudge_x = 1, nudge_y = 120) + # Добавляем подписи
  theme_classic(base_family = 'Merriweather', base_size = 12) + # более аккуратная тема для графика
  scale_size_continuous(range = c(3, 15)) + # Размеры кружочков
  transition_time(as.Date(Date)) + # Изменение положения и размера кружочков во времени
  labs(y = 'Площадь в процессе застройки, млн. м2', x = 'Индекс цен на недвижимость, г/г.', # Подписи
       title = 'Стоимость недвижимости и динамика строительства',
       subtitle = '{frame_time}', # Изменяющийся подзаголовок
       caption = '*Размер кружка - относительный ВРП на душу населения')

animate(p, height = 6, width = 8, units = "in", res = 200, duration = 70,
        fps = 30, end_pause = 50, render = av_renderer("anim_construction.mp4"))

Мы хотим проверить, как рост цен на жильё влияет на динамику строительства. Проблема в том, что в выборке разные регионы, которые между собой заметно отличаются и это может повлиять на результат. Учесть неоднородность регионов в выборке поможет модель с фиксированными эффектами.

Теория

Допустим, наша модель имеет вид:

\(y = \alpha + \beta_1 x + \beta_2z + \varepsilon\)

Где \(x\) - наблюдаемые переменные. \(z\) - ненаблюдаемые переменные, но те, которые мы хотели бы учесть, и мы знаем, что они важные.

yay

Как мы помним из лекции об инструментальных переменных, в таких случаях оценки МНК - смещённые:(

Смещённость - свойства оценки, которое появляется, если \(\theta \neq \mathbb{E}\theta\), т.е. ожидаемая ошибка (на выборке) в статистической модели не равна нулю.

  • Не меняющаяся во времени гетерогенность \(z\). С ней бороться очень просто. Если \(z\) во времени не меняется, то \(z_t = z_{t-1}\) и так далее.

Пример!

Тогда мы можем оценить модель в дифференциалах (first difference) в следующей форме и получить корректные оценки:

\[ \begin{align} \Delta y_t = \\ &= y_t - y_{t-1} \\ &= [\alpha + \beta_1 x_t + \beta_2z_t + \varepsilon_t] - [\alpha + \beta_1 x_{t-1} + \beta_2z_{t-1} + \varepsilon_{t-1}]\\ &=\beta_1[x_t - x_{t-1}] + \epsilon_t\\ &=\beta_1\Delta x_t + \epsilon_t \end{align} \] Другая стратегия - оценить МНК модель с дамми переменными для каждой индивида/группы/страны. Так делали в старину и лучше обходить стороной эту идею.

Намного лучше - модель с фиксированными эффектами. Что мы делаем: * Для независимой и зависимой переменной вычитаем для каждого индивида/страны/группы среднее значение переменной для индивида/страны/группы.

\[y_{it} - \bar{y}_{it} = [x_{it} - \bar{x}_n]\beta + [\varepsilon_{it} -\bar{\varepsilon}_i]\] Иногда ещё делят на стандартное отклонение, чтобы получить нормальную случайную величину с дисперсией 1, но это не всегда необходимо.

Давайте рассмотрим более общий случай:

\[ \begin{align} y_{it} &= X_{it}\beta + \varepsilon_{it}\\ &= X_{it}\beta + \eta_i + \nu_{it} \end{align} \] Где: * \(\eta_i\) - индивидуальный эффект, * \(\eta_i\) - остаточный эффект.

Далее можно просто показать табличку с панельными данными.

  • Within variation - то, как индивид/страна меняется во времени.
  • Between variation - то, как один индивид/страна отличается от остальных в выборке.

В fixed effects мы контролируем between variation

Теперь проверим наши гипотезы и сравним модели, где индивидуальные характеристики регионов не учтены (МНК) и модель с фиксированными эффектами:

ols <- lm(S_unf_redone ~ Population + HPI + CPI + GRP_pc, data = data_housing) # МНК
FE <- plm(S_unf_redone ~ Population + HPI + CPI + GRP_pc, data = data_housing,
          index = c("Region"), model ="within") # Модель с фиксированными эффектами

stargazer(ols, FE, type = 'html', header = FALSE) # Сравнение моделей
Dependent variable:
S_unf_redone
OLS panel
linear
(1) (2)
Population 0.0003*** 0.001***
(0.00000) (0.0001)
HPI 1.399*** 0.608**
(0.369) (0.294)
CPI 0.466 -4.931***
(1.424) (1.260)
GRP_pc 0.002*** 0.001***
(0.0001) (0.0002)
Constant -450.052***
(149.046)
Observations 5,472 5,472
R2 0.587 0.102
Adjusted R2 0.587 0.089
Residual Std. Error 406.077 (df = 5467)
F Statistic 1,945.608*** (df = 4; 5467) 152.772*** (df = 4; 5396)
Note: p<0.1; p<0.05; p<0.01

Как мы видим, модель с фиксированными эффектами намного успешнее уловила влияние инфляции (CPI) на строительство. В остальном, обе модели подтверждают гипотезу о том, что рост спроса на жильё в регионе увеличивает цены на недвижимость. Затем застройщики пытаются компенсировать неравновесное состояние на рынке жилья, увеличивая интенсивность строительства.

Пример 2

Экономическое развитие и продолжительность жизни

Данные:

gm <- read.csv('https://raw.githubusercontent.com/ETymch/Econometrics_2023/main/Datasets/gapminder.csv') %>%
  as_tibble() %>%
  mutate(log_GDPperCap = log(gdpPercap)) %>%
  group_by(country) %>%
  mutate(lifeExp_within = lifeExp - mean(lifeExp),
         log_GDPperCap_within = log_GDPperCap - mean(log_GDPperCap)) %>%
  ungroup()
gm %>% head()
# A tibble: 6 × 10
      X country     continent  year lifeExp      pop gdpPercap log_GDPperCap
  <int> <chr>       <chr>     <int>   <dbl>    <int>     <dbl>         <dbl>
1     1 Afghanistan Asia       1952    28.8  8425333      779.          6.66
2     2 Afghanistan Asia       1957    30.3  9240934      821.          6.71
3     3 Afghanistan Asia       1962    32.0 10267083      853.          6.75
4     4 Afghanistan Asia       1967    34.0 11537966      836.          6.73
5     5 Afghanistan Asia       1972    36.1 13079460      740.          6.61
6     6 Afghanistan Asia       1977    38.4 14880372      786.          6.67
# ℹ 2 more variables: lifeExp_within <dbl>, log_GDPperCap_within <dbl>

У нас есть данные о ВВП на душу населения и ожидаемой продолжительности жизни более чем в 100 странах на временном промежутке с 1952 по 2007 гг. с интервалом 5 лет. Мы хотим измерить, как экономическое развитие влияет на ожидаемую продолжительность жизни.

  • Снова имеем индивидуальную гетерогенность. Страны разнятся в культуре, географии, предрасположенности к болезням, представлениями о гигиене и пр.
  • Данных об этих межстрановых различия у нас нет:(
  • Тем не менее, Мы можем предположить, что все эти эффекты (межстрановые различия, названные выше) - фиксированные эффекты.

Давайте изобразим данные! Изобразить на одном графике данные по всем странам - сложно. На лекции мы проголосовали за 4 страны:

gm %>%
  filter(country %in% c('France', 'Korea, Dem. Rep.', 'Korea, Rep.', 'Albania')) %>%
  ggplot(aes(x = lifeExp_within, y = log_GDPperCap_within, color = country)) +
  geom_point(size = 5, alpha = 0.5) +
  theme_minimal() +
  facet_wrap(~country)

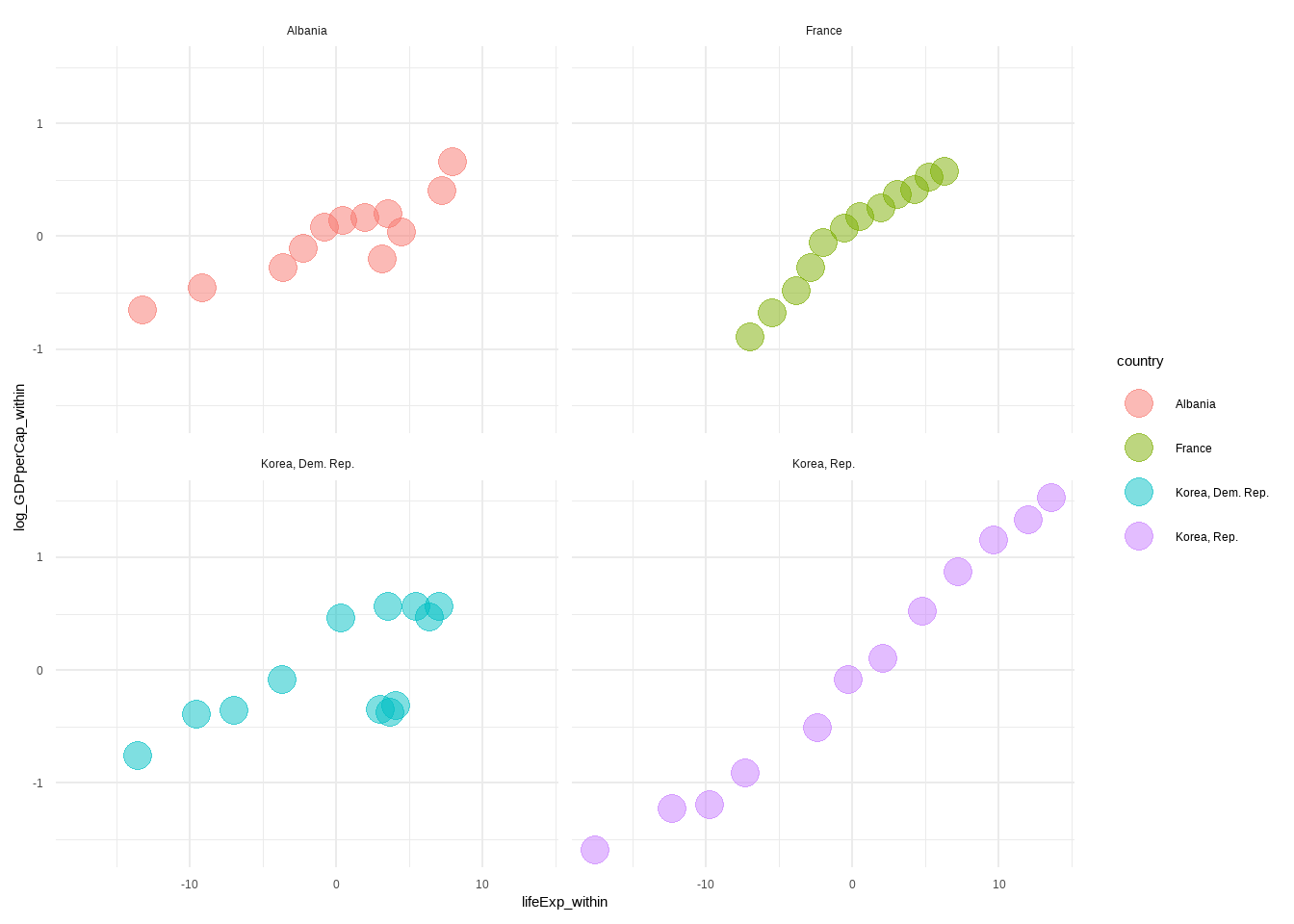
Оценим модель:

mod_0 <- lm(lifeExp ~ log_GDPperCap, gm)
mod_1 <- plm(lifeExp ~ log_GDPperCap, gm, index = c('country'))

stargazer(mod_0, mod_1, type = 'html', header = FALSE)
Dependent variable:
lifeExp
OLS panel
linear
(1) (2)
log_GDPperCap 8.405*** 9.769***
(0.149) (0.297)
Constant -9.101***
(1.228)
Observations 1,704 1,704
R2 0.652 0.410
Adjusted R2 0.652 0.356
Residual Std. Error 7.620 (df = 1702)
F Statistic 3,192.273*** (df = 1; 1702) 1,085.295*** (df = 1; 1561)
Note: p<0.1; p<0.05; p<0.01

Заметьте, мы получили очень большой эффект экономического развития на продолжительность жизни! Наш результат говорит, что удвоение ВВП на душу населения приводит к увеличению ожидаемой продолжительности жизни на 9 лет. Дело в переменных, которые мы пропустили! Выборка охватывает временной промежуток более 50 лет и за это время значительно изменилось состояние медицины, общемировое представление о гигиене и другие факторы, подверженные влиянию технического прогресса. Как это можно учесть в модели, чтобы получить более точные оценки параметров?

Для решения этой проблемы мы можем использовать двусторонние фиксированные эффекты. Мы предполагаем, что существует также гетерогенность во времени. Тогда мы также вводим дамми для каждого периода.

\[ y_{it} = \alpha_i + \alpha_t + X_{it}\beta + \varepsilon_{it} \] Оценим модель с двусторонними фиксированными эффектами:

mod_2 <- plm(lifeExp ~ log_GDPperCap, gm, index = c('country', 'year'), effect = 'twoways')

stargazer(mod_0, mod_1, mod_2, type = 'html', header = FALSE)
Dependent variable:
lifeExp
OLS panel
linear
(1) (2) (3)
log_GDPperCap 8.405*** 9.769*** 1.450***
(0.149) (0.297) (0.268)
Constant -9.101***
(1.228)
Observations 1,704 1,704 1,704
R2 0.652 0.410 0.019
Adjusted R2 0.652 0.356 -0.078
Residual Std. Error 7.620 (df = 1702)
F Statistic 3,192.273*** (df = 1; 1702) 1,085.295*** (df = 1; 1561) 29.366*** (df = 1; 1550)
Note: p<0.1; p<0.05; p<0.01

По сравнению с обыкновенной моделью с фиксированными эффектами, коэффициент, отвечающий за влияние экономического роста на ожидаемую продолжительность жизни в модели с двусторонними эффектами уменьшился приблизительно в 6 раз, тем не менее, он остался значимым! После того, как мы учли межвременную неоднородность, нам удалось более точно выделить влияние факторов, связанных с экономическим ростом на ожидаемую продолжительность жизни и получить значительно более достоверный результат!

Пример 3.

Банковские кризисы в отсутствие паники

bank runs

Данные пример основан на статье Baron et al. в QJE за 2020 год. В ней авторы исследуют случаи, когда активы банков теряли в цене, за этим следовало сокращение кредитования и экономический спад. Дело в том, что в макроэкономике банковские кризисы часто связывают с паникой заложили эту традицию Diamond, D., Dybvig, P., когда вкладчики стремятся забрать из банков свои накопления. У банков не хватает резервов, чтобы осуществить выплаты по всем вкладам и случается кризис и экономический спад. на выборке по 46 странам с 1870 по 2016 гг. авторы доказывают, что основной первопричиной банковских кризисов является не паника вкладчиков, а сокращение активов банков.

Они ставят вопросы:

  • Влияют ли существенные снижения ликвидности капиталов банков на макроэкономическую активность?
  • Является ли паника на банковском рынке необходимым условием для возникновения негативных среднесрочных последствий для макроэкономики?

\[ \Delta GDP_{t+h} = \alpha + \beta BankEquities_t + \beta Panic_t + \gamma X_{t,...,t+h} + \varepsilon_{t+h} \] Давайте проверим и мы!

data <- rio::import('https://github.com/ETymch/Econometrics_2023/raw/main/Datasets/BVX_annual_regdata.dta')

Давайте посмотрим, существует ли какая-либо зависимость между паникой на банковском рынке и сокращением банковских активов. Выберем 4 случайных страны:

data %>%
  filter(country %in% c('Italy', 'Spain', 'Austria', 'Argentina')) %>%
  ggplot(aes(x = Rtot_real_w, y = PANIC_ind)) +
  geom_point(color = '#ad466c', size = 2, alpha = 0.6) +
  facet_wrap(~country) +
  theme_bw(base_family = 'Lobster', base_size = 10) +
  labs(x = 'Индекс реальной доходности собственного капитала банка',
       y = 'Паника')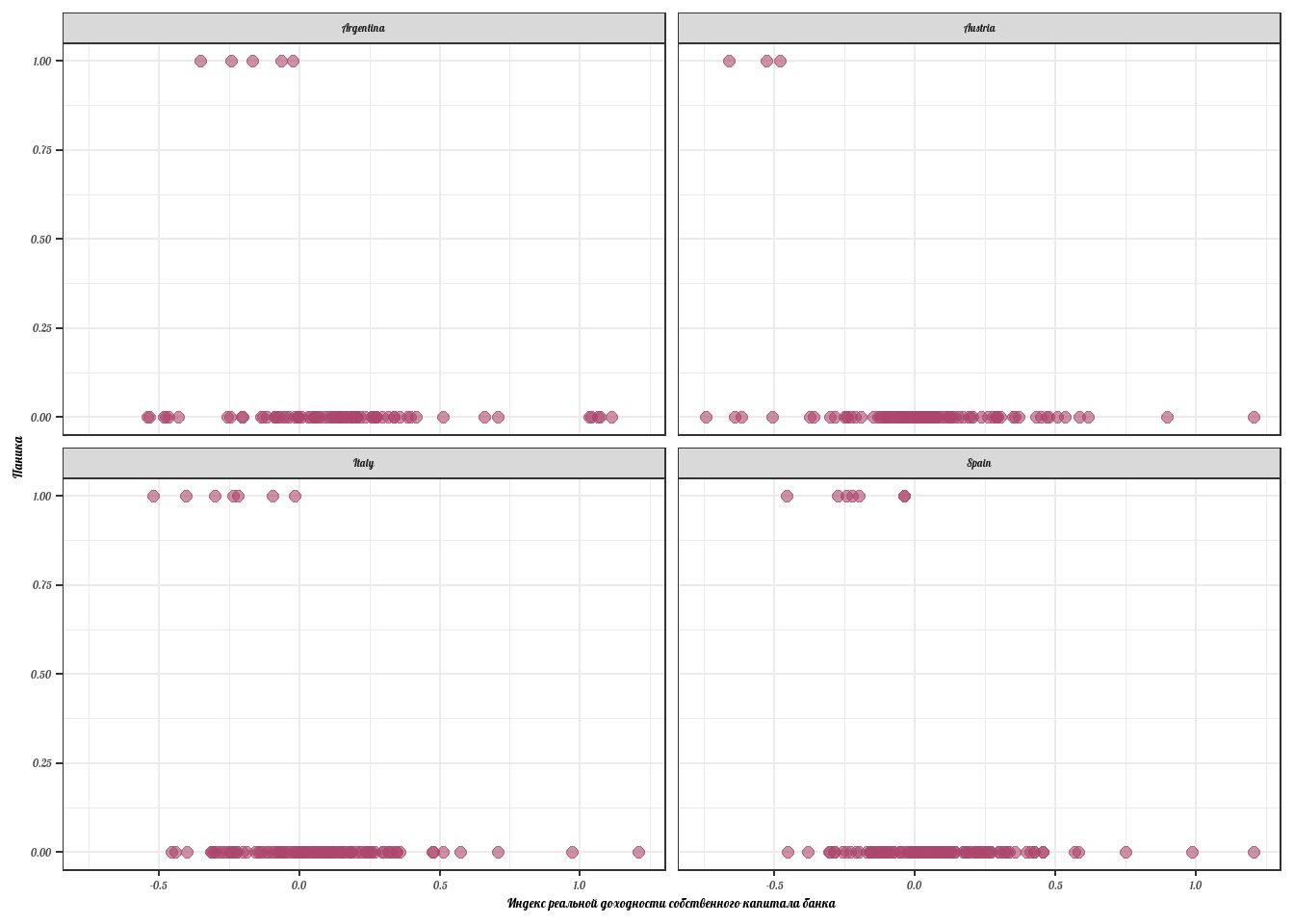

В данном случае мы опускаем существование межвременной гетерогенности и оцениваем две модели: обыкновенную модель, не учитывающую межстрановые различия и модель с индивидуальными фиксированными эффектами.

Переменные:

  • g3y - среднее значение роста выпуска в последующие 3 года.
  • Rtot_real_w - индекс реальной доходности собственного капитала банка.
  • PANIC_ind - индикатор паники на банковском рынке.
mod_0 <- plm(g3y ~ Rtot_real_w + PANIC_ind, data, model = 'within', index = c('country'))
mod_0_ols <- lm(g3y ~ Rtot_real_w + PANIC_ind, data)

stargazer(mod_0_ols, mod_0, type = 'html', header = FALSE)
Dependent variable:
g3y
OLS panel
linear
(1) (2)
Rtot_real_w 0.047*** 0.044***
(0.006) (0.006)
PANIC_ind -0.068*** -0.068***
(0.010) (0.009)
Constant 0.129***
(0.002)
Observations 3,786 3,786
R2 0.034 0.036
Adjusted R2 0.033 0.024
Residual Std. Error 0.112 (df = 3783)
F Statistic 65.805*** (df = 2; 3783) 70.577*** (df = 2; 3738)
Note: p<0.1; p<0.05; p<0.01

В данном случае, даже короткая регрессия помогла нам получить глубокий теоретический результат: * Даже в отсутствии паники, снижение стоимости активов банков приводит к существенному снижению кредитования, что приводит к снижению экономической активности. * Таким образом, невозможно объяснять финансовые кризисы лишь паникой, возникающей на финансовых рынках. Снижение выпуска имеет и иные причины, зачастую более важные, чем поведенческие.