Лекция 5

R
Автор

Е. Тымченко

Дата публикации

11 июля 2023 г.

Повторение: Метод максимального правдоподобия

Идея метода наименьших квадратов:

\[ \min_\beta (y - \mathbb{E}[y|X])^2 = \min_\beta(y - X\beta)^2 \]

Идея ММП:

\[\max_\beta \mathbb{P}(данные \sim какое-то распределение|\beta)\] Примеры:

  • Логистическая регрессия
  • Мультиномимльная логистическая регрессия
  • Пуассоновская регрессия

Пример: аренда велосипедов

Rent

У нас есть данные об аренде ведосипедов в городе Вашингтон на протяжении нескольких лет. Мы хотим посстроить модель, способную прогнозировать аренду на основе данных о погоде.

Нам потребуются библиотеки:

library(tidyverse) # Работа с данными
library(ggExtra) # Красивые типы  графиков
library(showtext) # Рендер шрифтов в ggplot2
library(sysfonts) # загрузка шрифтов в R
library(stargazer) # Удобные таблицы статистики моделей.
library(reshape2) # Для преобразования данных
library(patchwork) # С помощью этой библиотеки мы модем делать различные выкладки графиков. Например, График_1 | График_2.
showtext_auto()

# Шрифты для графиков
font_add_google('Lobster')
font_add_google('Cormorant SC')

# Любимый цвет для графиков
col1 <- '#ad466c'

Загрузка данных:

bikes_train <- read.csv('https://github.com/ETymch/Econometrics_2023/raw/main/Datasets/bikes_train.csv')
bikes_test <- read.csv('https://github.com/ETymch/Econometrics_2023/raw/main/Datasets/bikes_test.csv')
b <- bikes_train %>%
  ggplot(aes(x = atemp, y = count)) +
  geom_jitter(color = col1, size = 3.0, alpha = 0.2) +
  theme_minimal(base_family = 'Lobster', base_size = 16) +
  labs(x = 'Температура, С', y = 'Число арендованных велосипедов')
ggMarginal(b, type="density", size = 5, fill = col1, alpha = 0.6, color = NA)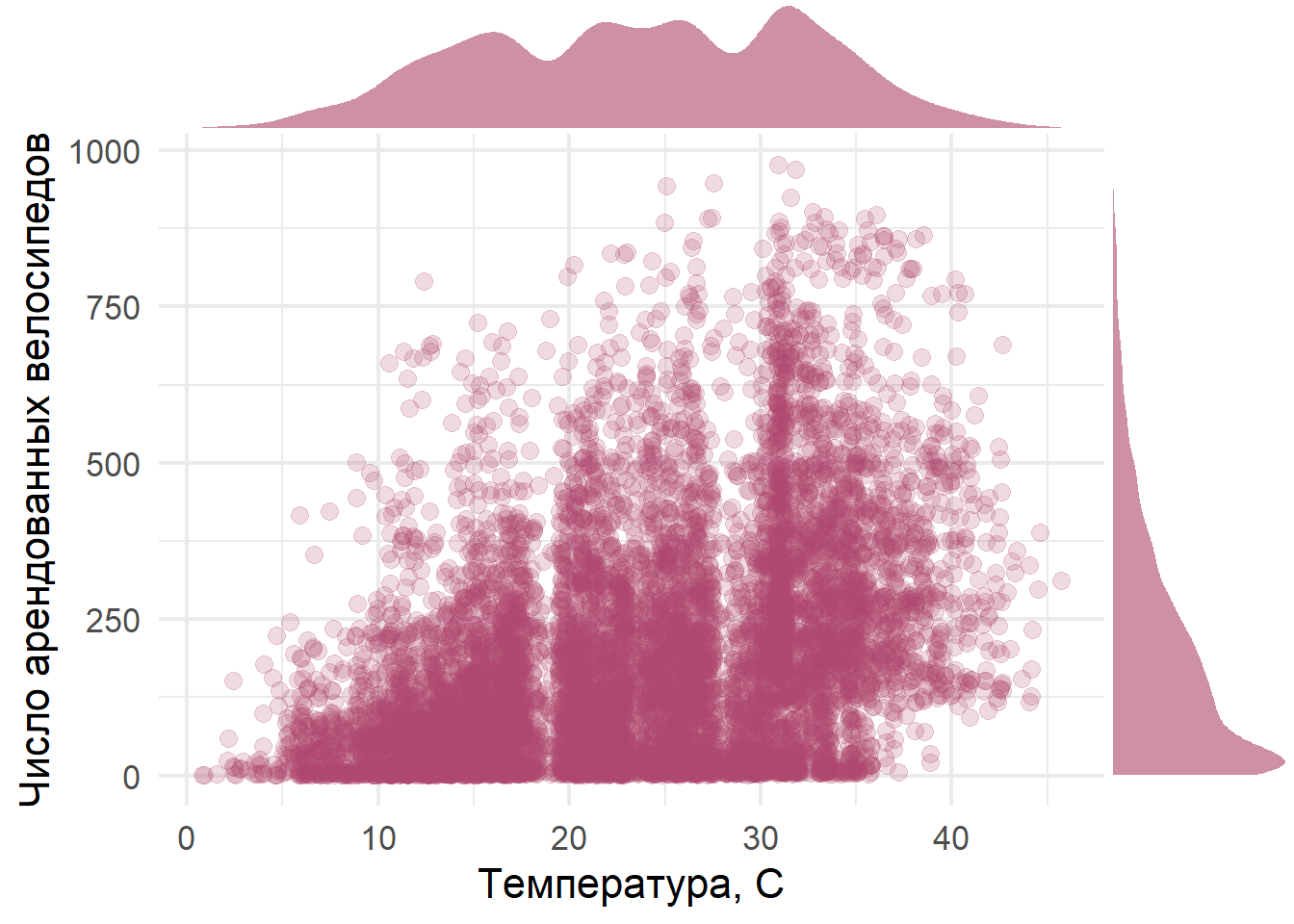

Оценим 4 модели, 3 из которых - пуассоновская регрессия о одна - МНК.

mod_0 <- glm(count ~ humidity + season, family = poisson, bikes_train)
mod_1 <-glm(count ~ humidity + season + atemp + windspeed, family = poisson, bikes_train)
mod_2 <-glm(count ~ humidity + season + atemp + windspeed + workingday, family = poisson, bikes_train)
mod_ols <-glm(count ~ humidity + season + atemp + windspeed + workingday, family = gaussian, bikes_train)

stargazer(mod_0, mod_1, mod_2, mod_ols, header = F, type = 'html')
Dependent variable:
count
Poisson normal
(1) (2) (3) (4)
humidity -0.018*** -0.015*** -0.015*** -2.992***
(0.00004) (0.00004) (0.00004) (0.092)
season 0.203*** 0.150*** 0.150*** 22.292***
(0.001) (0.001) (0.001) (1.573)
atemp 0.037*** 0.037*** 7.308***
(0.0001) (0.0001) (0.203)
windspeed 0.006*** 0.006*** 1.052***
(0.0001) (0.0001) (0.214)
workingday 0.004** -0.166
(0.002) (3.547)
Constant 5.817*** 4.760*** 4.757*** 135.229***
(0.003) (0.004) (0.005) (9.284)
Observations 9,000 9,000 9,000 9,000
Log Likelihood -655,441.500 -573,657.500 -573,654.200 -58,246.660
Akaike Inf. Crit. 1,310,889.000 1,147,325.000 1,147,320.000 116,505.300
Note: p<0.1; p<0.05; p<0.01

Прогнозы для тестовой выборки:

pr_0 <- predict(mod_0, bikes_test %>% select(-count)) %>% exp()
pr_1 <- predict(mod_1, bikes_test %>% select(-count)) %>% exp()
pr_2 <- predict(mod_2, bikes_test %>% select(-count)) %>% exp()
pr_ols <- predict(mod_ols, bikes_test %>% select(-count))

# Сводная таблица со всеми данными

result <- 
  tibble(pr_0, # прогнозы моделей
       pr_1,
       pr_2,
       pr_ols,
       true_value = bikes_test$count, # истинные значения
       id = seq(1, length(pr_0), by = 1)) %>% # номер наблюдения
  mutate(error_0 = (pr_0 - true_value)^2, # квадраты ошибок
         erroe_1 = (pr_1 - true_value)^2,
         error_2 = (pr_2 - true_value)^2,
         error_ols = (pr_ols - true_value)^2
  )

Статистика ошибок в четырёх моделях.

result %>%
  select(error_0,
         erroe_1,
         error_2,
         error_ols) %>%
  sapply(mean) %>% # Применить функцию "среднее" к каждому столбцу
  sapply(sqrt) # Применить функцию "Квадратный корень" к каждому столбцу
  error_0   erroe_1   error_2 error_ols 
 163.2686  152.1845  152.1992  152.5746

На основании данных о средних ошибках мы не понимаем, какая модель лучше описывает данные. Давайте посмотрим, насколько равномерно распределены ошибки в зависимости от истинных значений аренды велосипедов.

p1 <- result %>%
  select(error_2, true_value) %>%
  filter(error_2 <= 100000) %>%
  ggplot(aes(x = error_2, y = true_value)) +
  geom_point(color = col1, alpha = 0.15, size = 2) +
  theme_minimal(base_family = 'Cormorant SC', base_size = 16) +
  labs(x = 'Ошибки в модели пуассоновской регрессии',
       y = 'Истинное значение')

p2 <- 
  result %>%
  select(error_ols, true_value) %>%
  filter(error_ols <= 100000) %>%
  ggplot(aes(x = error_ols, y = true_value)) +
  geom_point(color = col1, alpha = 0.15, size = 2) +
  theme_minimal(base_family = 'Cormorant SC', base_size = 16) +
  labs(x = 'Ошибки в модели, оценённой МНК',
       y = 'Истинное значение')

p1 | p2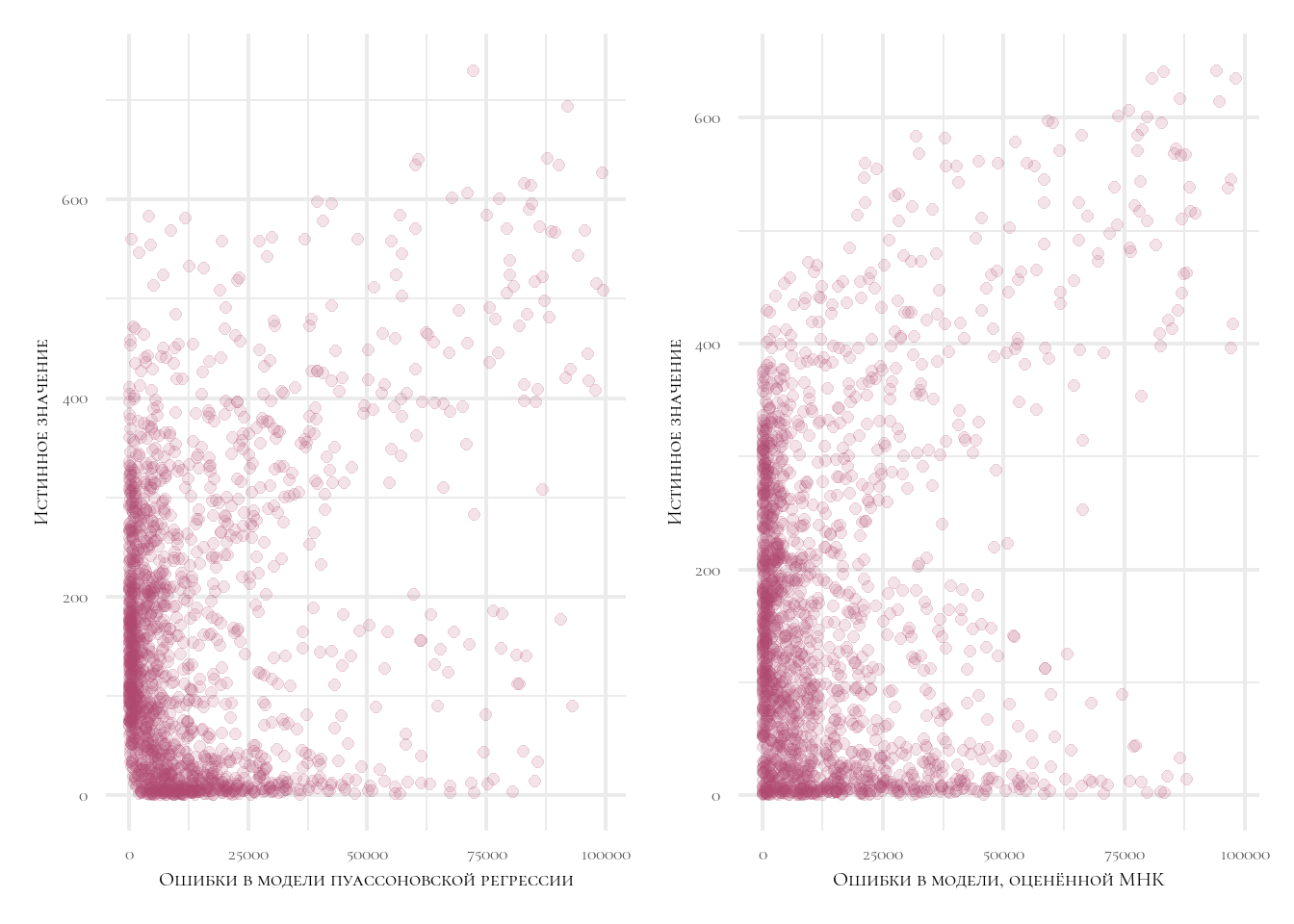

Мы видим, что в модели пуассоновской регрессии ошибки распределены более равномерно!

Инструментальные переменные

Angrist (1990)

  • Добровольцы,
  • Отобранные повредством лотереи.

Лотереи - идеальный естественнный эксперимент

draft
  • 366 шкриков. На каждом - день рождения (1 янв = 1, и так далее).
  • Ведущий по очереди вытаскивает шарики.
  • Порядок вытащенных номеров формирует призывную очередь.
  • Дамми: высокий выбор на драфте и низкий выбор на драфте.

\[y_i = \alpha + \beta M_i + \ldots + \varepsilon_i\] \(M_i = 0\), если учавствовал. \(M_i = 1\), если не участвовал.

Проблема!

\(M_i\) связан с ненаблюдаемыми переменными, влияющими на доходы. Но возможно, что эти люди пошли в армию, а значит оценки Теорема Гаусса-Маркова не работает и оценки МНК - не лучшие из возможных.

Почему \(M_i\) связан с \(\varepsilon_i\)?

Самоотбор: вероятно, в армию отбираются люди, менее заинтересованные в больших деньгах и офисной работе.

Из-за этой связи оценки МНК будут больше (по модулю), чем истинные оценки влияния военной службы на доходы.

Как это влияет на оценки параметров?

\[\hat{\beta} = \frac{dy}{dx} = \frac{\partial y}{\partial x} + \frac{\partial \varepsilon}{\partial x} \] Вспомните, ТГМ предполагает полное отсутствие связи между \(x\) и ошибками в модели. Если данное предположение нарушается, то оценки \(\hat{\beta}\) становятся смещёнными:

Рисунок

\[ \begin{align} \hat{\beta} \\ &= \frac{dy}{dx} \\ &= \frac{\partial y}{\partial x} + \frac{\partial \varepsilon}{\partial x} \\ &= \beta + \phi \end{align} \]

Где \(\beta\) - истинное влияние \(x\) на \(y\), \(\hat{\beta}\) - оценка МНК. \(\phi\) - влияние упущенной информации \(\varepsilon\) на \(x\) \(\gamma\) - влияние \(x\) на \(\varepsilon\)

Оценка с помощью инструментальных переменных:

Нужно найти такую переменную \(z\), которая влияет на \(x\), но не влияет на \(\varepsilon\). Так:

\[\frac{\partial y}{\partial z} = \frac{\partial y}{\partial x} \frac{\partial x}{\partial z} + 0\]

\[\beta_{IV} = \frac{\partial y / \partial z}{\partial x / \partial z}\]

Рисунок

Структурная оценка против сокращённой:

  • Необходимость микрообоснований.
  • Пример: статья Keane в JOE. Альтернативные объяснения - изменение услий, вкладываемых в образование и поиск работы при получении высокого номера на драфте.
  • 2SLS, пример: налоги.