Лекция 4 - практическая часть
Библиотеки
Данные
Сегодня мы построим модель, которая позволит диагностировать сахарный диабет, на основании различных данных о пациенте.
Почему в данном случае МНК - не лучший вариант для оценки параметров?
Наиболее значимым фактором для постановки такого диагноза является уровень глюкозы в крови. Построим график зависимости диагноза от кровня глюкозы:
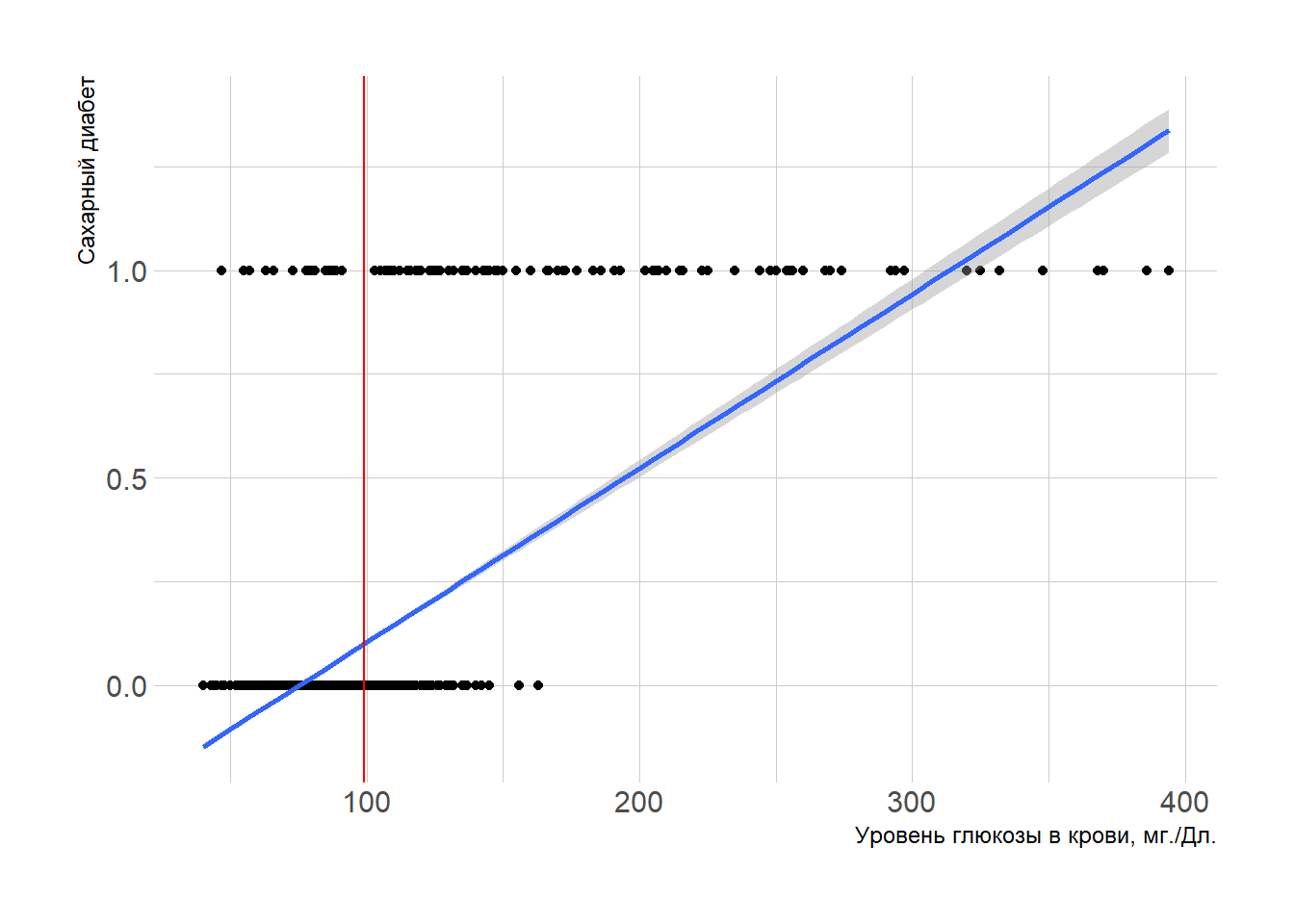
Линия плохо описывает взаимосвязь. Возможно, такая форма лучше?
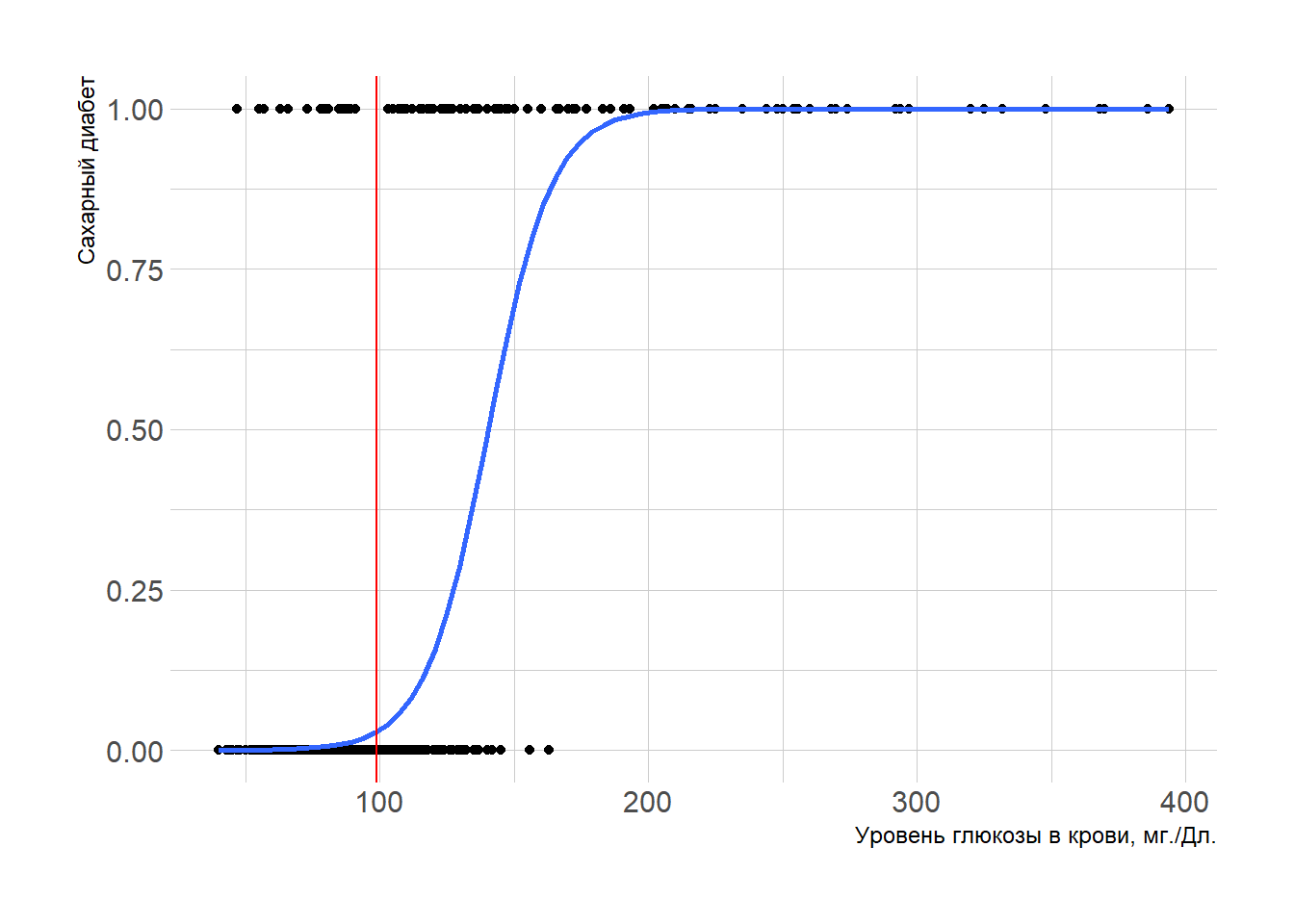
Оценим модель с помощью МНК.
| Dependent variable: | |
| diabetes | |
| glucose | 0.004*** |
| (0.0001) | |
| Constant | -0.323*** |
| (0.008) | |
| Observations | 3,116 |
| R2 | 0.375 |
| Adjusted R2 | 0.375 |
| Residual Std. Error | 0.130 (df = 3114) |
| F Statistic | 1,870.258*** (df = 1; 3114) |
| Note: | p<0.1; p<0.05; p<0.01 |
Но как её интерпретировать? Что значит отрицательный intercept? Если человек не сдавал анализ на глюкозу, его заболеваемость отрицательная? Также, вспомните Теорему Гауccа-Маркова, в которой сказано, что если выполнены несколько условий, одним из которых является линейность связи между зависимой и независимой переменной, то оценка МНК - лучшая несмещённая оценка. В нашем случае связь, очевидно, нелинейная, а оценки МНК - не лучшие. А значит нам нужен иной метод - Метод Максимального Правдоподобия.
Для оценки таких моделей у нас есть более удачная функция, чем обыкновенная прямая. Эта функция - сигмоид.
Логистическая функция
Напишем уравнение для линии.
Уравнение логистической функции.
Параметры и интервал
Теперь нарисуем их:
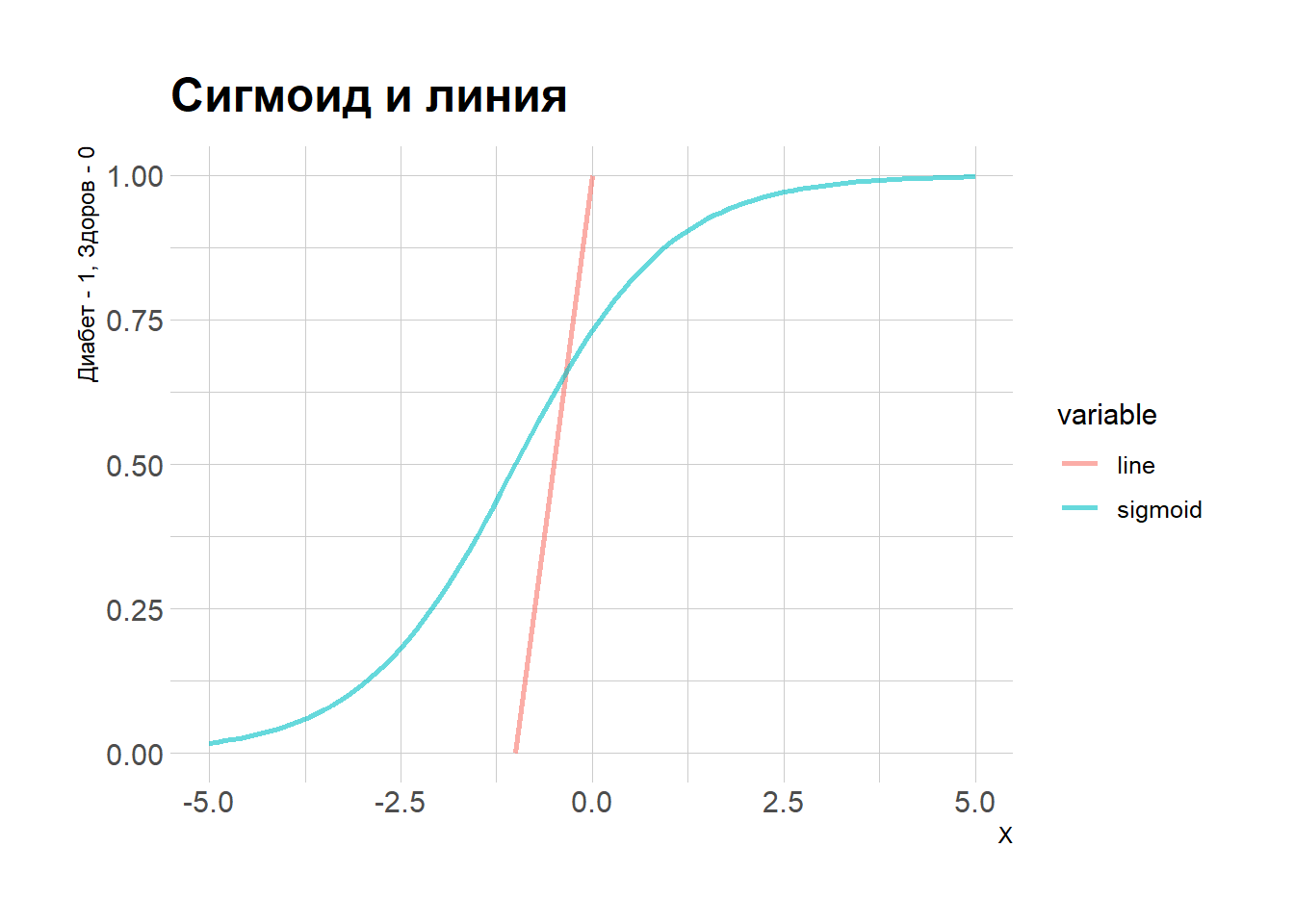
Чтобы получить больше интеиции о том, как устроена логистическая функция, Сравним две модели:
- МНК: \(y_i = intercept + \beta_1 x_i + \epsilon_i\)
- Логистическая регрессия: \(y_i = \frac{1}{1 + e^{-(intercept + \beta_1 x_i)}} + \epsilon_i\)
Зафиксируем \(\beta_1\) и посмотрим, что произойдёт при изменении intercept.
Теперь зафиксируем intercept и посмотрим, что будет при изменении \(\beta_1\):
Оценим две модели:
| Dependent variable: | ||
| diabetes | ||
| OLS | logistic | |
| (1) | (2) | |
| glucose | 0.004*** | 0.083*** |
| (0.0001) | (0.007) | |
| Constant | -0.323*** | -11.732*** |
| (0.008) | (0.720) | |
| Observations | 3,116 | 3,116 |
| R2 | 0.375 | |
| Adjusted R2 | 0.375 | |
| Log Likelihood | -185.367 | |
| Akaike Inf. Crit. | 374.735 | |
| Residual Std. Error | 0.130 (df = 3114) | |
| F Statistic | 1,870.258*** (df = 1; 3114) | |
| Note: | p<0.1; p<0.05; p<0.01 | |
Ставим диагнозы при помощи модели
S <- function(x){
1 / (1 + exp(- (coefficients(mod_ml)[1] + coefficients(mod_ml)[2] * x)))
}
y <- function(x){
coefficients(mod_ols)[1] + coefficients(mod_ols)[2]*x
}
gl_test <- test$glucose # Столбец с значением анализа для тестовой выборки.
dia_test <- test$diabetes # Столбец с истинным значением диагноза.
# Создаём табличку
result <- tibble(gl_test,
dia_test,
pred_ols = y(gl_test),
pred_ml = S(gl_test)) %>%
mutate(pred_ml_01 = ifelse(pred_ml < 0.5, 0, 1)) # создайм ещё одну переменную со значением прогноза на основе предсказанной вероятности.
result %>%
head(10) # посмотрим на вервые 10 строк в таблице.# A tibble: 10 × 5
gl_test dia_test pred_ols pred_ml pred_ml_01
<dbl> <dbl> <dbl> <dbl> <dbl>
1 166 1 0.387 0.892 1
2 79 0 0.0152 0.00581 0
3 120 1 0.191 0.151 0
4 75 0 -0.00195 0.00417 0
5 72 0 -0.0148 0.00325 0
6 78 0 0.0109 0.00534 0
7 68 0 -0.0319 0.00233 0
8 67 0 -0.0362 0.00214 0
9 80 0 0.0194 0.00631 0
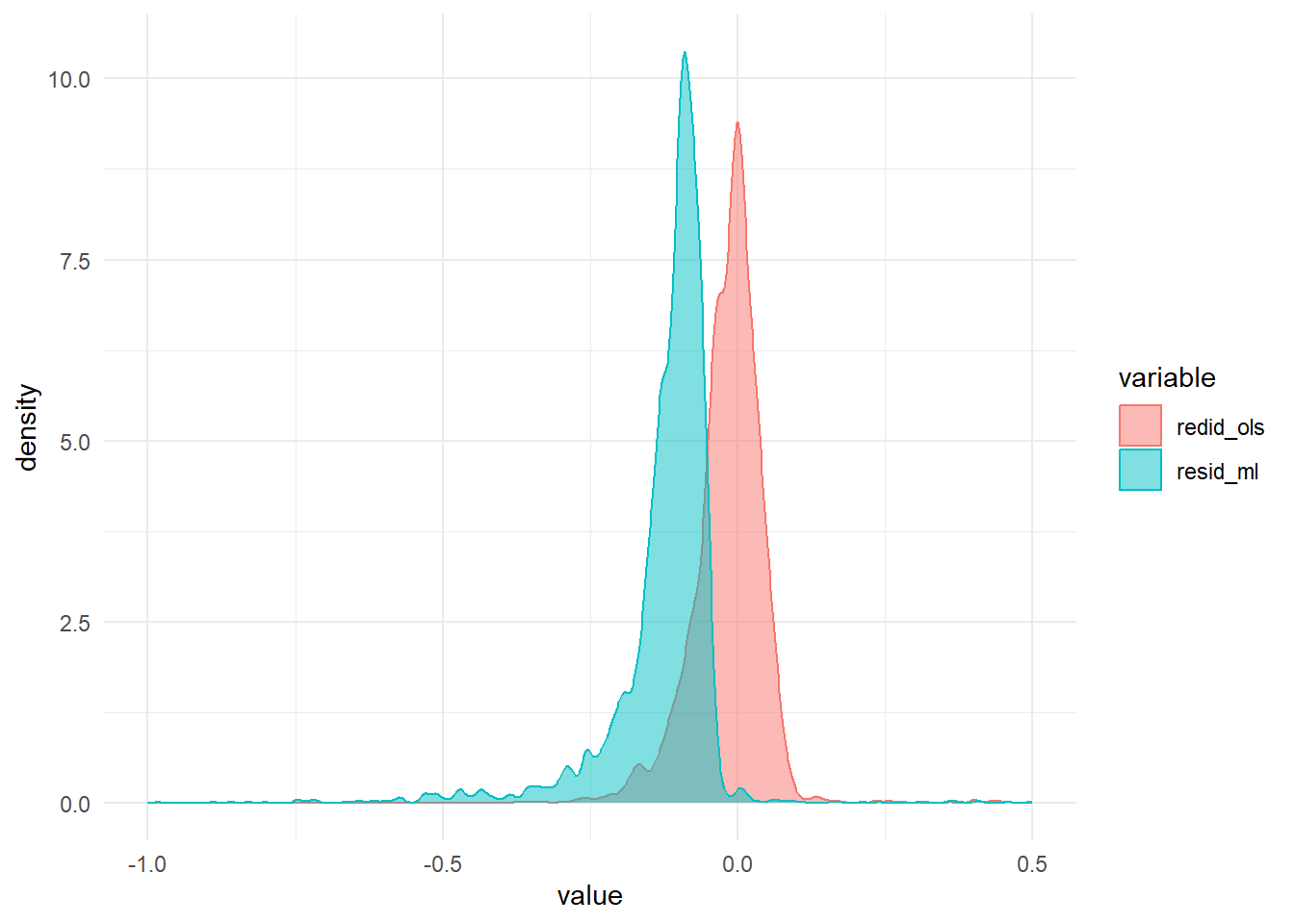
10 74 0 -0.00622 0.00383 0В отличие от оценок, сделанных при помощи МНК, оценки ММП смещённые. Это значит, что средняя ошибка в модели не равна 0.
[1] -3.123725e-17[1] -0.09042032Для большей наглядности, нарисуем распределение ошибок в моделях:
Добавим в модель больше параметров и сравним с первой:
| Dependent variable: | ||
| diabetes | ||
| (1) | (2) | |
| glucose | 0.083*** | 0.082*** |
| (0.007) | (0.007) | |
| age | 0.048** | |
| (0.021) | ||
| education | -0.055 | |
| (0.163) | ||
| cigsPerDay | -0.008 | |
| (0.016) | ||
| totChol | 0.003 | |
| (0.003) | ||
| Constant | -11.732*** | -14.682*** |
| (0.720) | (1.523) | |
| Observations | 3,116 | 3,018 |
| Log Likelihood | -185.367 | -174.440 |
| Akaike Inf. Crit. | 374.735 | 360.880 |
| Note: | p<0.1; p<0.05; p<0.01 | |
Сравним, какая модель стваит диагнозы: с однйо объясняющей переменной или с несколькими:
S <- function(x){
1 / (1 + exp(-x))
}
predict_ml <- predict(mod_ml, test %>% select(-diabetes)) %>%
S()
predict_ml_1 <- predict(mod_ml_1, test %>% select(-diabetes)) %>%
S()
predictions <- tibble(true_diagnoses = test$diabetes,
prob_ml = predict_ml,
prob_ml_1 = predict_ml_1) %>%
mutate(dia_ml = ifelse(prob_ml < 0.5, 0, 1),
dia_ml_1 = ifelse(prob_ml_1 < 0.5, 0, 1)
) %>%
mutate(error_ml = ifelse(dia_ml == true_diagnoses, 0, 1),
error_ml_1 = ifelse(dia_ml == true_diagnoses, 0, 1)
)
predictions %>%
tail(10) # последние 10 наблюдений в табличке# A tibble: 10 × 7
true_diagnoses prob_ml prob_ml_1 dia_ml dia_ml_1 error_ml error_ml_1
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0 NA NA NA NA NA NA
2 0 0.0156 0.0249 0 0 0 0
3 0 0.00353 0.00360 0 0 0 0
4 0 0.00275 0.00159 0 0 0 0
5 0 NA NA NA NA NA NA
6 0 0.00453 0.00195 0 0 0 0
7 0 0.00181 0.00105 0 0 0 0
8 0 0.0170 0.00856 0 0 0 0
9 0 0.00214 0.00105 0 0 0 0
10 0 0.00534 0.00526 0 0 0 0Удивительно, но обе модели ошиблись в диагнозах менее 20 раз из 800 - менее 5%! Модель с одной объясняющей переменной показала отличную способность прогнозировать диагнозы, потому что мы выбрали наиболее значимую объясняющую переменную - уровень инсулина.