Лекция 3

Автор

Е. Тымченко

Дата публикации

14 июня 2023 г.

Сегодня мы поупражняемся в тестировании гипотез при помощи ранее изученной теории.

Нам понадобятся библиотеки:

library(wooldridge) # Библиотека с датасетами из учебника Introductory Econometrics by J. Wooldridge. 
library(tidyverse) # Для работы с табличками в R, рисования и написания кода
library(stargazer) # Красивые таблицы со статистикой регрессий

library(hrbrthemes) # Темы для графиков ggplot2, попробуйте `+theme_ipsum()`
library(showtext) # Для рендера шрифтов в ggplot2.
library(sysfonts) # Для загрузки шрифтов из google fonts. Найдите шрифты, которые вам по душе https://fonts.google.com/.
font_add_google('Merriweather') # так мы можем загрузить шрифт из google fonts
showtext.auto() # Для использования библиотеки showtext для рендера шрифта по-умолчанию.

Для анализа мы будем использовать данные из статьи Hamermesh, D.S. and J.E. Biddle (1994), в которой авторы эмпирически тестировали трудовую дискриминацию в пользу более привлекательных людей. А также то, что этот эффект существует и значим как для мужчин, так и для женщин. Наш набор данных переработан автором учебника и включает лишь часть данных, использованных в статье, что не мешает нам протестировать гипотезы из статьи. Подробную информацию о данных можно получить, набрав ?wooldridge::beauty.

data <- beauty # Загружаем наш набор данных

Для начала, давайте проверим, есть ли вообще какая-либо разница между доходами более привлекательных и менее привлекательных людей. В данных есть переменная, отвечающая за внешнюю привлекательность - looks, которая принимает значения от 1 до 5. Если looks принимает значение 1 или 2, мы говорим, что внешняя привлекательность человека ниже среднего (below average или сокращённо belavg). Давайте сравним средние зарплаты для групп с внешней привлекательностью ниже среднего (belavg == 1) и прочими участниками исследования (belavg == 0)

data_l <- data %>%
  filter(belavg == 1) # Часть данных, в которой переменная belavg = 1 (привлекательность ниже средней)
data_h <- setdiff(data, data_l) # Остальные участники (belavg = 0)

s <- mean(data_h$lwage) - mean(data_l$lwage) # разница между заработными платами более привлекательных и менее привлекательных людей
s

[1] 0.1930406

Предположим, что на самом деле эта разница в 0.19 получилась в нашей выборке случайно и привлекательность на заработные платы не влияет. Тогда мы можем случайным образом разбить наши исходные данные на 2 кусочка, посчитать разницу между средними заработными платами в этих кусочках и получить 0.19 много раз. Это бы значило, что в нашей выборке разница 0.19 между средними зп более привлекательных и менее привлекательных людей не значима и заработные платы скорее всего не связаны с внешним обаянием. Проведём такой тест

stat <- c() # создаём пустой вектор
for (i in 1:1000){ # Запускаем петлю с 1000 итераций.
data_0 <- sample_n(data, 155) # Случайным образом выбираем 155 наблюдений выборки
data_1 <- setdiff(data, data_0) # Дополнение data_0 до выборки.

stat[i] <- mean(data_1$lwage) - mean(data_0$lwage) # Разница в средних заработных платах между двумя выборками
}

Мы получили вектор stat, состоящий из 1000 наблюдений. Каждое наблюдение - разница между средними заработными платами в случайном разбиении нашей выборки на 2. Теперь мы можем построить график в ggplot2.

Построим график в ggplot

tibble(result = stat) %>% # Создаём табличку с нашим вектором stat.
  ggplot(aes(x = result)) + # aes - ось. В данном случае мы отобразим наш вектор stat (result), по горизонтальной оси x.
  geom_density(alpha = 0.2, fill = 'orange', color = NA) + # мы хотим нарисовать функцию плотности
  theme_ipsum() + # Красивая тема из библиотеки hrbrthemes.
  labs(title = 'Красота имеет значение',
       x = 'Плотность',
       y = 'Логарифм заработных плат') + # Добавим подписи осей и название
  geom_vline(xintercept = mean(stat)) + # Вертикальная линия, среднее разницы зп в нашем численном эксперименте 
  geom_vline(xintercept = s, color = 'red', linetype = 'dotted', size = 1.2) # Разница заработных плат между более привлекательными и менее привлекательными людьми в выборке.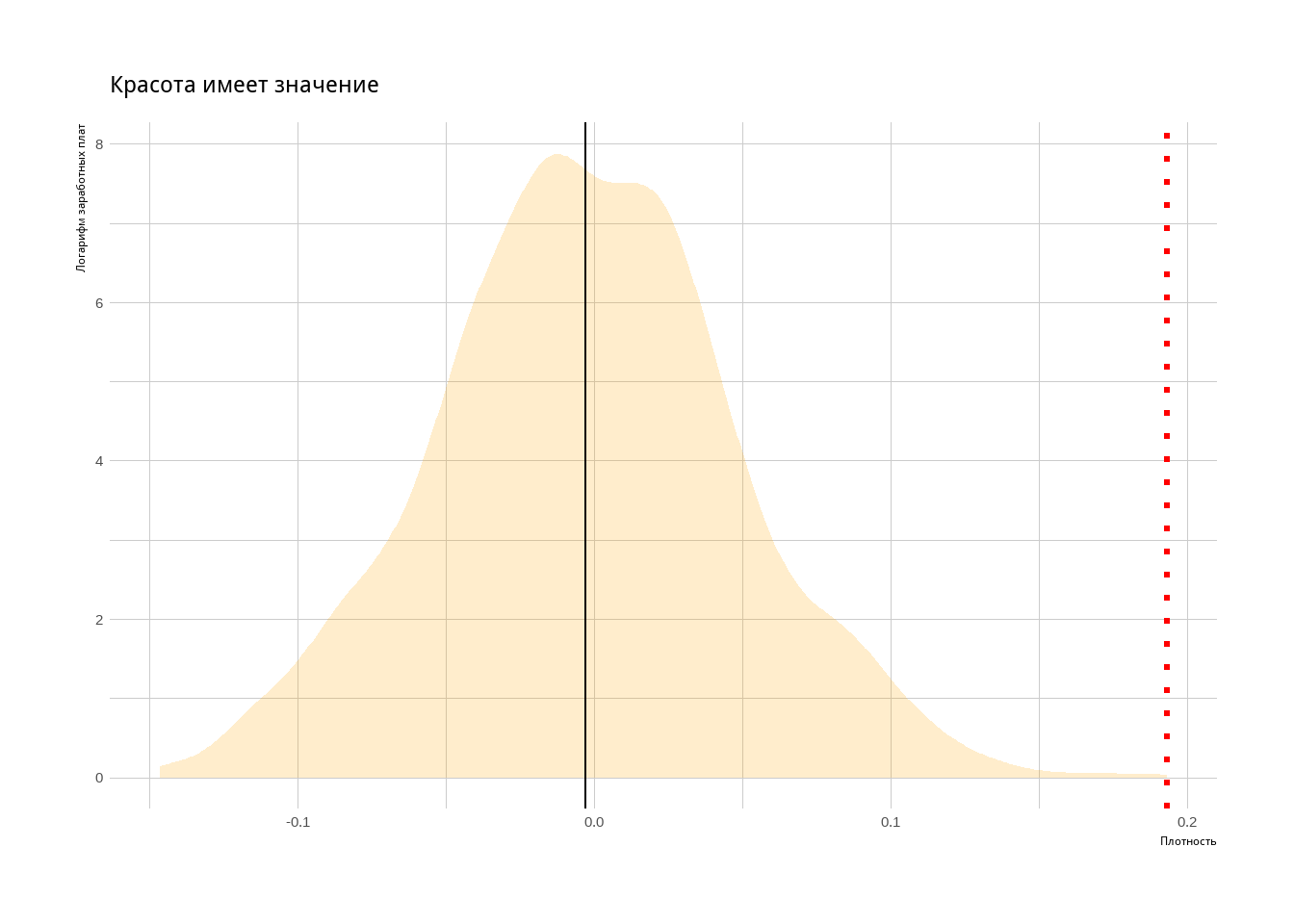

Данный результат можно получить, оценив модель с одной объясняющей переменной методом наименьших квадратов.

\[lwage_i = \alpha + \beta belavg_i + \epsilon_i\]

mod_0 <- lm(lwage ~ belavg, data) # линейная модель с одно объясняющей переменной.

mod_0 %>% summary # Описательная статистика к нашей модели. Обратите внимание, значение коэффициента при belavg в точности равно 0.19!


Call:
lm(formula = lwage ~ belavg, data = data)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.66274 -0.36079  0.01307  0.38895  2.67057 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.68255    0.01779  94.581  < 2e-16 ***
belavg      -0.19304    0.05072  -3.806 0.000148 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.5913 on 1258 degrees of freedom
Multiple R-squared:  0.01138,   Adjusted R-squared:  0.0106 
F-statistic: 14.49 on 1 and 1258 DF,  p-value: 0.000148

Описательная статистика предлагает нам много информации о коэффициентах регрессии и прилагающейся к ним статистике. Например, Std. Error для полученных нами коэффициентов. Давайте разберёмся, что это значит. Дело в том, что мы можем думать о коэффициентах регрессии (\(\beta\)), как о случайных величинах, которые тоже имеют какое-то распределение. Это распределение мы можем получить при помощи Бутстрапa. Бутстрап - очень простой, и вместе с тем, очень полезный и значимый для современной статистики алгоритм. Допустим, мы хотим узнать распределение коэффициента \(\beta\) при переменной belavg. Чтобы это сделать, нужно всего-навсего:

Выбрать случайным образом (с возвращением, т.е. какое-то наблюдение можно выбрать несколько раз) какое-то кол-во наблюдений из нашей выборки (назовём это подвыборкой).
Оценить на этой подвыборке нашу регрессионную модель \(lwage_i = \alpha + \beta belavg_i + \epsilon\).
Записать значение коэффициента \(\beta\).
Слелать это несколько тысяч раз.
Тогда записанные нами значения \(\beta\) и будут распределением нашего коэффициента.
По центральной предельной теореме, при увеличении количества наблюдений в подвыборке (из пункта 1), распределение \(\beta\) всё больше напоминает нормально распределение с параметрами \((\hat{\beta}, Std. Error^2)\).

Само собой, мы можем вывести формулу для стандартного отклонения коэффициентов аналитически. На мой взгляд, это излишне и не даёт ученикам нужной интуиции при первом знакомстве с предметом.

stat_1 <- c() # пустой вектор, куда мы будем записывать значения коэффициентов.
for (i in 1:3000){ # проведём эксперимент 3000 раз!
samp <- sample_n(data, 1500, replace = T) # Выберем случайным образом 1500 наблюдений из нашей выборки с 1260 наблюдений (да, мы можем себе это позволить, потому что выбираем мы с возвращением (одно наблюдение может быть выбрано несколько раз)). При увеличении числа наблюдений с 1500 до большего числа распределение нашего итогового результата будет стремиться к нормальному с параметрами (b, std. error).
mod <- lm(lwage ~ belavg, samp) # Оцениваем мнк модель для нашей подвыборки
stat_1[i] <- mod$coefficients[2] # Записываем получившийся коэффициент в вектор
} # Повторяем 3000 раз.

sd(stat_1) # стандартное отклонение случайной величины

[1] 0.04572821

mean(stat_1) # среднее

[1] -0.1919479

Проверим гипотезу 1:

При прочих равных менее привлекательные люди зарабатывают меньше, чем более красивые.

Для этого нам нужно построить и проанализировать регрессионную модель

\[lwage_i = \alpha + \beta_1 looks_i + \beta_2 exper_i + \beta_3 educ_i + \beta_4 bigcity_i + beta_5 black_i + \epsilon_i\] В которой:

lwage - логарифм заработных плат.
looks - значение внешней привлекательности от 1 до 5.
exper - опыт работы в годах (предполагается, что более опытные сотрудники получают бОльшие заработные платы).
educ - кол-во лет, проведённых за получением образования (предполагается, что более образованные люди получают большую заработную плату).
bigcity - крупный ли город, где человек работает (предполагается, что в крупных городах заработные платы выше)
black = 1, если участник опроса чернокожий. Иначе 0. Мы включили этот параметр, чтобы учесть социальные факторы, влияющие на заработные платы.

mod_1 <- lm(lwage ~ looks + exper + educ + bigcity + black, data) # полная модель
mod_2 <- lm(lwage ~ looks, data) # укороченная модель

stargazer(mod_0, mod_1, type = 'html', header = FALSE) # функция stargazer из одноимённой библиотеки позволяет нам строить такие красивые таблички и использовать их в отчётах, публикациях и пр.


	Dependent variable:

	lwage
	(1)	(2)

belavg	-0.193^***
	(0.051)

looks		0.061^***
		(0.022)

exper		0.018^***
		(0.001)

educ		0.066^***
		(0.006)

bigcity		0.209^***
		(0.036)

black		-0.208^***
		(0.057)

Constant	1.683^***	0.275^***
	(0.018)	(0.104)


Observations	1,260	1,260
R²	0.011	0.232
Adjusted R²	0.011	0.229
Residual Std. Error	0.591 (df = 1258)	0.522 (df = 1254)
F Statistic	14.485^*** (df = 1; 1258)	75.661^*** (df = 5; 1254)

Note:	p<0.1; p<0.05; p<0.01

Значимые наблюдения:

В эконометрических исследованиях норма, когда выборка не репрезентативная. Иначе говоря, не представляет собой идеальный срез генеральной совокупности. Бывает, что в выборку попадают наблюдения, заметно отличающиеся от всех прочих, вероятность появления которых в действительности значительно меньше той, с которой оно попало в нашу выборку (1/число наблюдений в выборке). Такие наблюдениявносят большой вклад в то, какими получаются коэффициенты регрессии. Бывает, что они искажают наши результаты. Объясним на примере:

stat_2 <- c() # создадим пустой вектор
for (i in 1:nrow(data)){ # для каждого наблюдения в ввыборке
mod <- lm(lwage ~ looks + exper + educ + bigcity + black, data[-i,]) # оценим регрессии для подвыборки (выборка за исключением этого наблюдения)
stat_2[i] <- sum(mod$residuals^2) # посчитаем сумму квадратов остатков
}

stat_2 <- stat_2 / mean(stat_2) # нормируем для удобства наш вектор

plot(stat_2)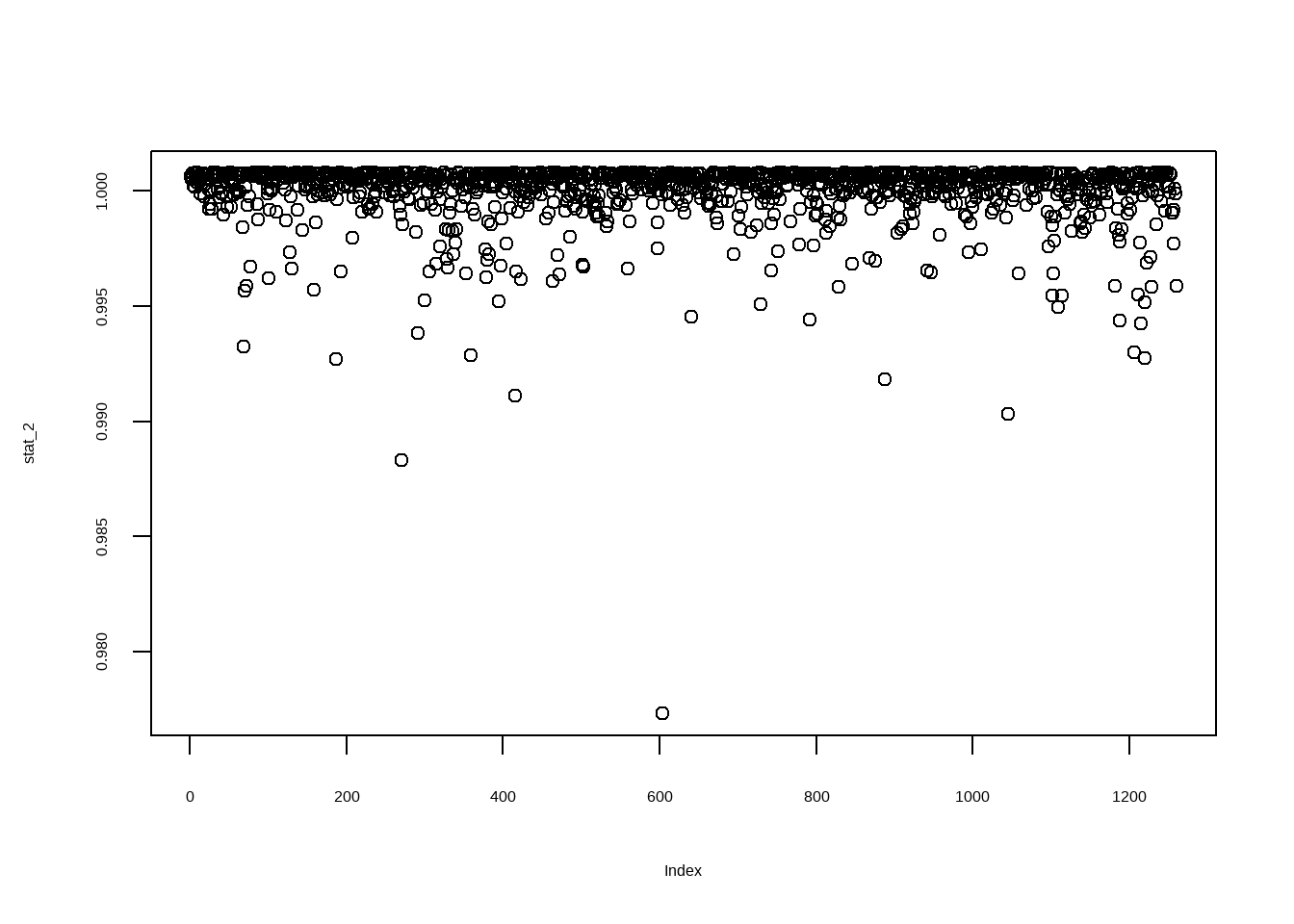

Мы видим, что если бы мы исключили 603 наблюдение, сумма квадратов остатков уменьшилась бы заметно. Это означает, что 603 наблюдение заметно отличается от прочих в нашей выборке. Давайте посмотрим на него:

data[603, ]

     wage    lwage belavg abvavg exper looks union goodhlth black female
603 77.72 4.353113      0      1     9     4     1        1     1      1
    married south bigcity smllcity service expersq educ
603       1     0       1        0       1      81   13

Действительно, мы имеем привлекательную замужнюю чернокожую женщину из большого города с заработной платой, значительно превосходящей всех прочих людей в выборке. Вероятно, она принадлежит к общественной группе, заметно отстоящей от индивидов в выборке.

mod_3 <- lm(lwage ~ looks + exper + educ + bigcity + black, data[-603,]) # Оценим ещё одну модель, но уже без 603 наблюдения
stargazer(mod_1, mod_2, mod_3, type = 'html', header = FALSE) # Удивительно, но даже одно наблюдение, если оно заметно отличается от прочих, может значительно влиять на получаемые нами коэффициенты.


	Dependent variable:

	lwage
	(1)	(2)	(3)

looks	0.061^***	0.051^**	0.058^***
	(0.022)	(0.024)	(0.022)

exper	0.018^***		0.018^***
	(0.001)		(0.001)

educ	0.066^***		0.066^***
	(0.006)		(0.006)

bigcity	0.209^***		0.201^***
	(0.036)		(0.036)

black	-0.208^***		-0.238^***
	(0.057)		(0.057)

Constant	0.275^***	1.496^***	0.286^***
	(0.104)	(0.080)	(0.102)


Observations	1,260	1,260	1,259
R²	0.232	0.003	0.237
Adjusted R²	0.229	0.003	0.234
Residual Std. Error	0.522 (df = 1254)	0.594 (df = 1258)	0.516 (df = 1253)
F Statistic	75.661^*** (df = 5; 1254)	4.349^** (df = 1; 1258)	77.987^*** (df = 5; 1253)

Note:	p<0.1; p<0.05; p<0.01

Проверим гипотезу 2:

Для женщин эффект привлекательности на заработные платы больше, чем для мужчин.

Давайте посмотрим, есть ли какая-либо разница в эффекте привлекательности на заработные платы, если мы оценим 2 модели: первую - для мужчин в нашей выборке, вторую - для женщин.

data_m <- data %>%
  filter(female == 0) # мужчины в выборке
data_f <- setdiff(data, data_m) # женщины в выборке

mod_m <- lm(lwage ~ looks + exper + educ + black + bigcity, data_m) # модель для мужчин
mod_f <- lm(lwage ~ looks + exper + educ + black + bigcity, data_f) # модель для женщин

mod_m$coefficients[2] - mod_f$coefficients[2]

        looks 
-0.0003200253

Чтобы проверить гипотезу, вновь воспользуемся бутстрапом. На сей раз статистика, которая нам нужна - разница между заработными коэффициентами \(\beta_1\) в двух моделях.

boot_lm <- function(data, n){
  stat <- c()
  for (i in 1:n){
  
  data_m <- data %>%
  sample_n(500)
  
  data_f <- setdiff(data, data_m)

mod_m <- lm(lwage ~ looks + exper + educ + black + bigcity, data_m)
mod_f <- lm(lwage ~ looks + exper + educ + black + bigcity, data_f)

stat[i] <- mod_m$coefficients[2] - mod_f$coefficients[2]
  }
  stat
}

Нарисуем результат:

st_boot <- boot_lm(data, 1000)
tibble(st_boot = st_boot) %>%
  ggplot(aes(x = st_boot)) + 
  geom_density(alpha = 0.2, fill = '#4D081F', color = NA) +
  theme_minimal(base_family = 'Merriweather') +
  labs(title = 'Мужская красота, как и женская, имеет значение', x = 'Разница между коэффициентами', y = 'Плотность')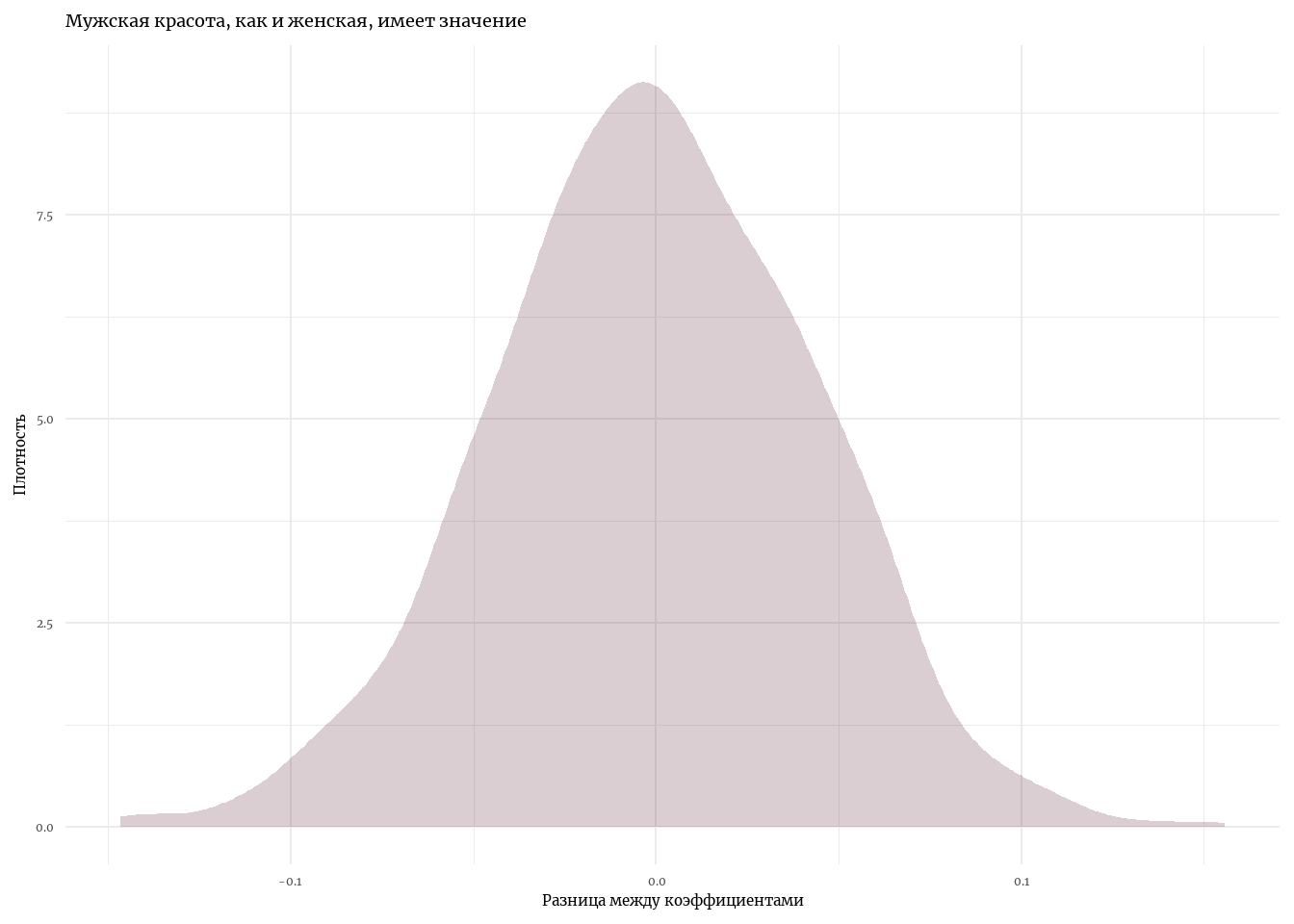

Мы можем заключить: внешняя привлекательность влияет на заработные платы мужчин точно так же, как на заработные платы женщин. Вместе с тем, мы видим, что ожидаемые заработные платы женщин при прочих равных ниже заработных плат мужчин.

mod_4 <- lm(lwage ~ looks + exper + educ + bigcity + black + female, data[-603,]) # добавим в модель переменную female.
stargazer(mod_1, mod_2, mod_3, mod_4, type = 'html', header = FALSE)


	Dependent variable:

	lwage
	(1)	(2)	(3)	(4)

looks	0.061^***	0.051^**	0.058^***	0.051^**
	(0.022)	(0.024)	(0.022)	(0.020)

exper	0.018^***		0.018^***	0.014^***
	(0.001)		(0.001)	(0.001)

educ	0.066^***		0.066^***	0.065^***
	(0.006)		(0.006)	(0.005)

bigcity	0.209^***		0.201^***	0.187^***
	(0.036)		(0.036)	(0.033)

black	-0.208^***		-0.238^***	-0.142^***
	(0.057)		(0.057)	(0.052)

female				-0.460^***
				(0.029)

Constant	0.275^***	1.496^***	0.286^***	0.564^***
	(0.104)	(0.080)	(0.102)	(0.095)


Observations	1,260	1,260	1,259	1,259
R²	0.232	0.003	0.237	0.365
Adjusted R²	0.229	0.003	0.234	0.362
Residual Std. Error	0.522 (df = 1254)	0.594 (df = 1258)	0.516 (df = 1253)	0.471 (df = 1252)
F Statistic	75.661^*** (df = 5; 1254)	4.349^** (df = 1; 1258)	77.987^*** (df = 5; 1253)	119.816^*** (df = 6; 1252)

Note:	p<0.1; p<0.05; p<0.01