Лекция 2
Цены на рынке подержанных автомобилей
- Чего мы хотим? Смоделировать ценообразование на рынке подержанных машин.
- В базе данных - 500 тысяч проданных на аукционе автомобилей в 2014-15 гг.
- Чтобы предмет исследования был однородным - выберем одну модель. В нашем случае - Ford Focus.

У нас есть теория, которую мы вывели логически, что цены подержанных автомобилей как-то зависят от их пробега. Запишем её:
\[ price_i = \beta_0 + \beta_1 o_i + \epsilon_i\]
где \(beta_0\) - цена новой машины. \(\beta_1\) - эластичность цены по пробегу.
Хорошо, у нас есть теоретическая модель, но как нам узнать \(\beta_1\) и \(\beta_2\) используя данные? Представьте, что вы никогда не читали учебника по эконометрике, но у вас есть базовые знания мат. статистики. Какое решение предложили бы вы?
Первой догадкой было бы просто посмотреть, как выглядит двухмерный график с нашими переменными.
data %>%
ggplot(aes(x = odometer, y = sellingprice)) +
geom_point(color = '#e5b9ad', fill = 'white', shape = 21, size = 1.5) +
geom_point(color = '#e5b9ad', fill = '#e5b9ad', shape = 21, size = 1.5, alpha = 0.2) +
theme_minimal(base_family = 'Yeseva One') +
labs(x = 'Пробег', y = 'Цена продажи') +
scale_x_continuous(limits = c(0, 300000), labels = label_number())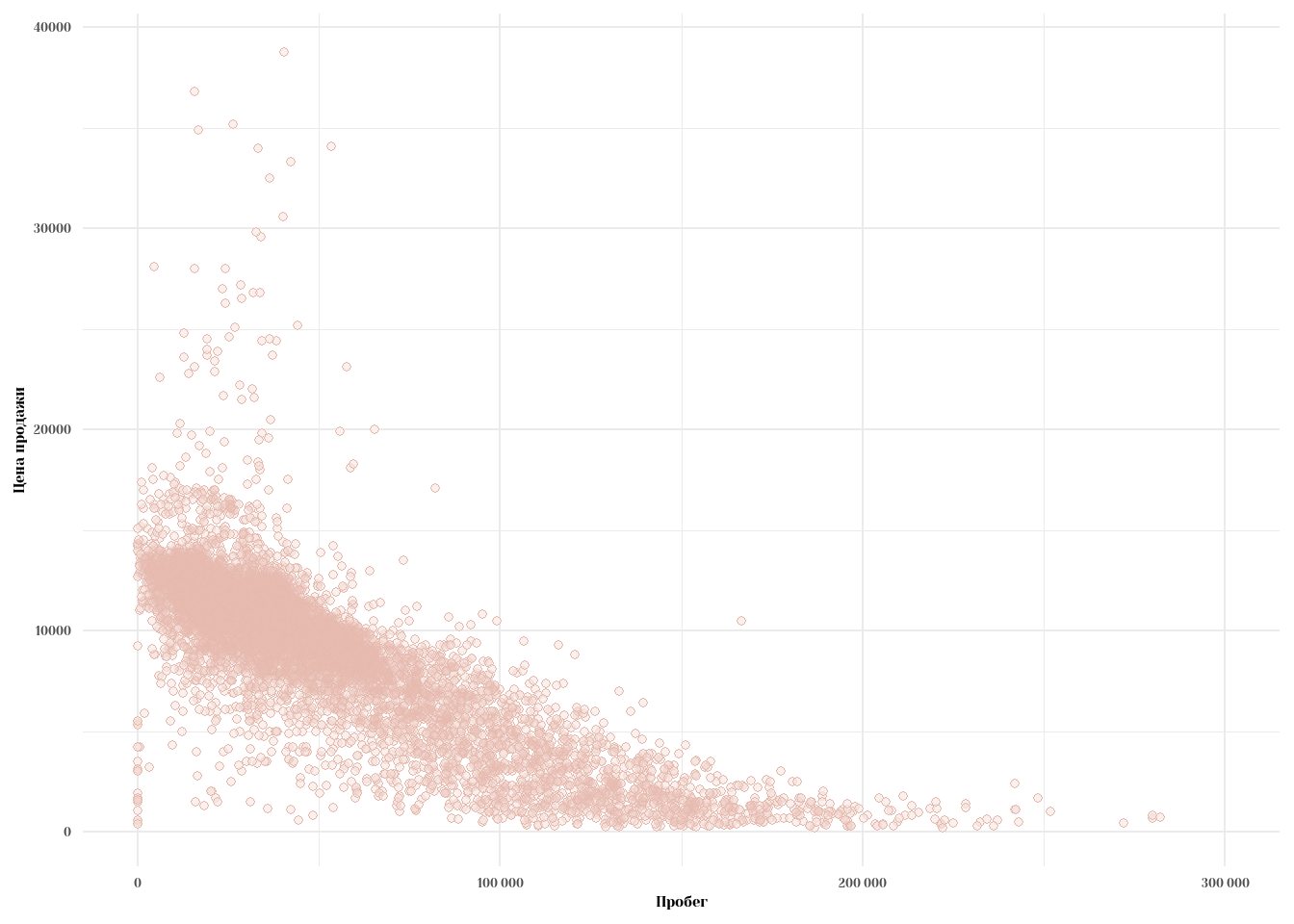
Очевидно, есть какая-то взаимосвязь, которая как-то похода на линейную. Заметьте, что при пробеге более 150 тысяч миль, цена принимает какое-то среднее маленькое значение, примерно постоянное на промежутке \(X \in (150000,300000)\).
Следующий шаг. Посмотрим, как распределены цены в нашей выборке.
price <- data$sellingprice %>%
na.omit() %>%
as.numeric() %>%
data.frame() %>%
set_names('price')
price %>%
ggplot() +
geom_histogram(mapping = aes(x = price),
col = 'skyblue',
fill = 'green', alpha = 0.3) +
theme_minimal(base_family = 'Lobster', base_size = 19) +
labs(x = 'Цены', y = 'Число наблюдений', title = 'Распределение цен в выборке')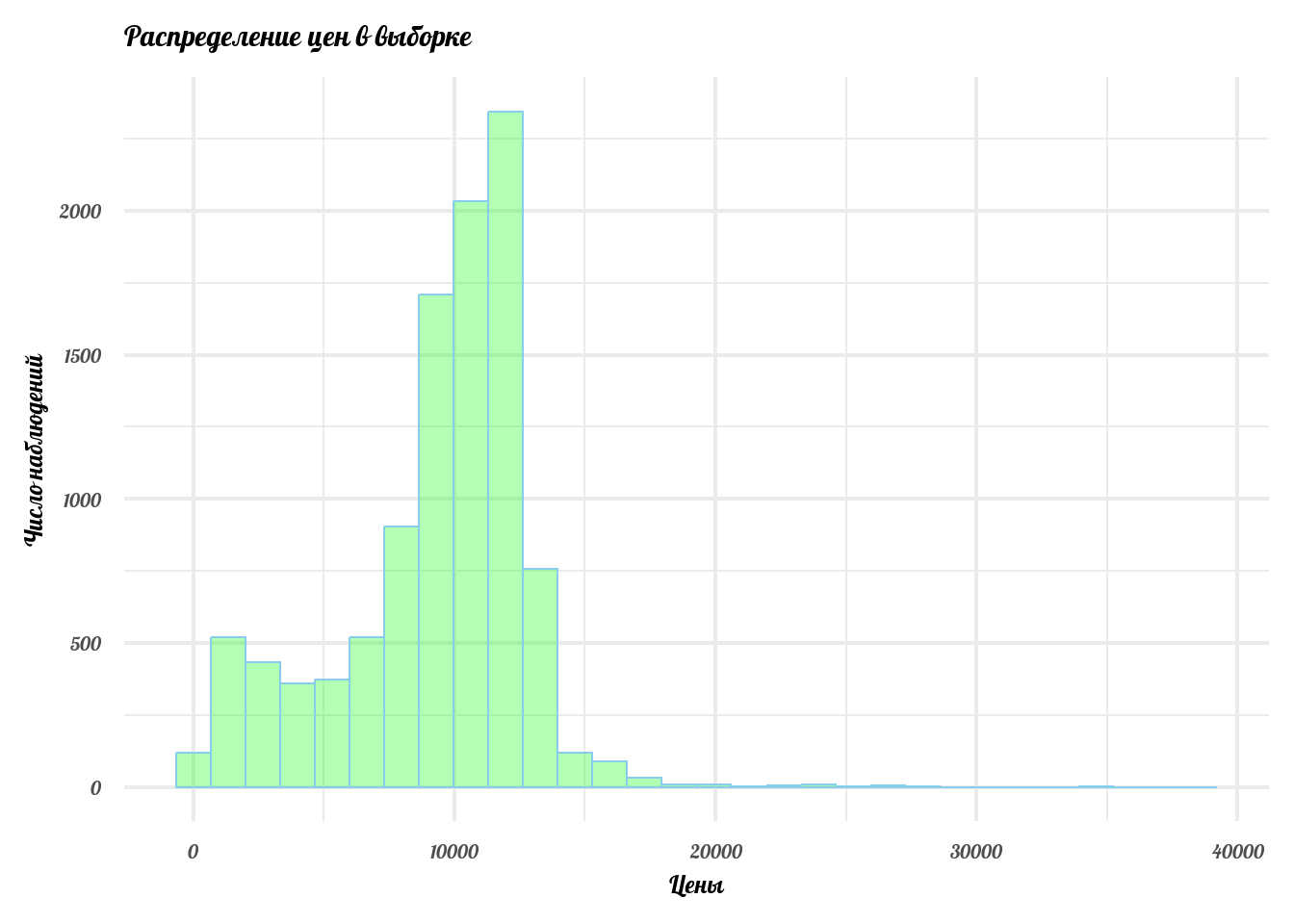
odometer <- data$odometer %>%
na.omit() %>%
as.numeric() %>%
data.frame() %>%
set_names('odometer')
odometer %>%
ggplot() +
geom_histogram(mapping = aes(x = odometer),
col = 'red',
fill = 'orange', alpha = 0.3) +
xlim(0,250000) +
theme_minimal(base_family = 'Lobster', base_size = 19) +
labs(x = 'Пробег', y = 'Число наблюдений', title = 'Распределение пробега в выборке')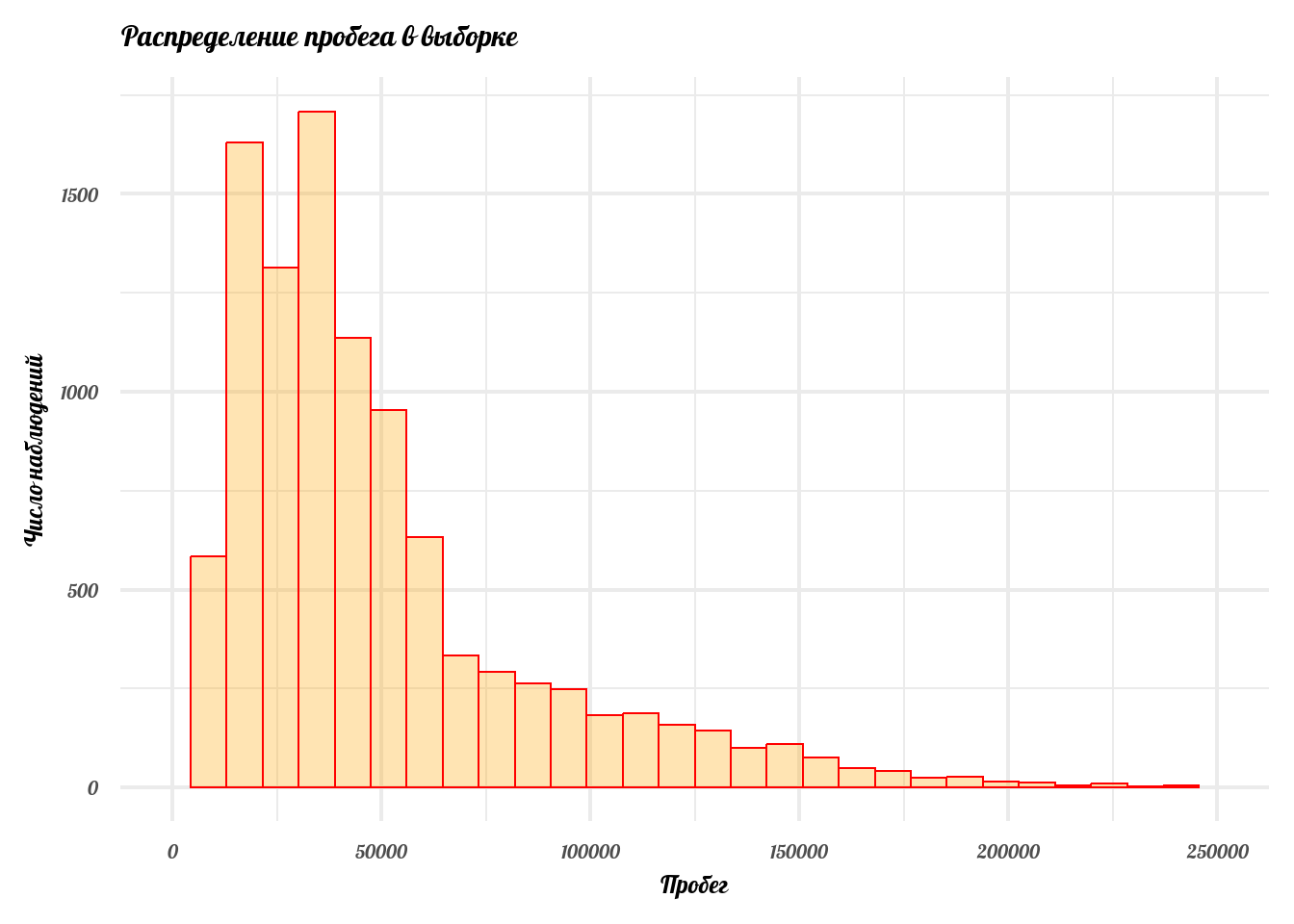
Случайные величины в экономике часто имеют странные распределения, на первый взгляд мало напоминающие нормальное. Мы обсуждали это на прошлой лекции. Чтобы частично это исправить, практики часто прибегают к трансформации исходных данных. Зачем это нужно?
Пример
Мы хотим прогнозировать \(Y\) на основании данных об \(X\). Мы придумали и логически обосновали модель: \[Y = \alpha + \beta X + \varepsilon\] так как (в классической статистике) параметры \(\alpha\) и \(\beta\) - числа, и если Y имеет, скажем, какое-нибудь странное несимметричное распределение, как цены в нашей выборке, а X - другое странное распределение, то \(\hat{\alpha} + \hat{\beta} X\) не будет хорошей оценкой для X. Для начала, давайте посмотрим, как выглядит линейная модель, если X и Y - нормальные случайные величины:
x <- rnorm(mean = 1, sd = 2, 1000)
y <- 3 + 2*x + rnorm(mean = 0, sd = 2, 1000)
model <- lm(y ~ x)
df <- data_frame(x = x,
alpha_plus_beta_x = model$coefficients[1] + x*model$coefficients[2]) %>%
melt()
df$variable <- c(rep(1, 1000), rep(2, 1000))
df %>%
ggplot(aes(x = value)) +
geom_density(fill = '#e5b9ad', color = '#e5b9ad', alpha = .5) +
geom_density(data = tibble(y), aes(x = y), fill = 'lightgreen', color = 'skyblue', alpha = 0.4) +
labs(x = 'Значения', y = '',
title = 'Линейная модель и функции плотности') +
theme_minimal(base_family = 'Yeseva One') +
theme(plot.title = element_text(size = 15, hjust = 0.5),
plot.subtitle = element_text(size = 15),
axis.text = element_text(size = 13),
axis.title = element_text(size = 14),
axis.ticks = element_blank(),
panel.background = element_blank()) +
guides(fill = 'none') +
ease_aes('linear') +
transition_time(variable)
Нормальные распределения имеют очень удобные характеристики. Именно поэтому при изложении предмета часто исходят из предпосылки о нормальности.
Пример
Теперь давайте посмотрим, как выглядит линейное отображение \(X\) в \(Y\), если они не нормальные. Например, как в нашем случае с подержанными автомобилями.
dat <- data %>%
na.omit()
model <- lm(data = dat, sellingprice ~ odometer)
dat_1 <- data_frame(x = dat$odometer,
alpha_plus_x = model$coefficients[1] + dat$odometer*model$coefficients[2]) %>%
melt()
dat_1$variable <- c(rep(1, length(dat$sellingprice)), rep(2, length(dat$sellingprice)))
dat_1 %>%
ggplot(aes(x = value)) +
geom_density(fill = '#e5b9ad', color = '#e5b9ad', alpha = .5) +
geom_density(data = dat, aes(x = sellingprice), fill = 'lightgreen', color = 'skyblue', alpha = 0.4) +
labs(x = 'Значения', y = '',
title = 'Линейная модель и функции плотности') +
theme_minimal(base_family = 'Yeseva One') +
theme(plot.title = element_text(size = 14, hjust = 0.5),
plot.subtitle = element_text(size = 15),
axis.text = element_text(size = 13),
axis.title = element_text(size = 13),
axis.ticks = element_blank(),
panel.background = element_blank()) +
guides(fill = 'none') +
ease_aes('linear') +
transition_time(variable) +
xlim(0, 75000)
Вопрос
Какие недостатки мы наблюдаем в парной регрессии, если \(X\) и \(Y\) распределены не нормально?
Вопрос
Как мы можем решить эту проблему? Нужно ли её вообще решать?
Анализировать такие случайные процессы часто помогает логарифмирование.
dat <- dat %>%
mutate(odometer = log(odometer),
sellingprice = log(sellingprice)
)
model <- lm(data = dat, sellingprice ~ odometer)
dat_1 <- data_frame(x = dat$odometer,
alpha_plus_x = model$coefficients[1] + dat$odometer*model$coefficients[2]) %>%
melt()
dat_1$variable <- c(rep(1, length(dat$sellingprice)), rep(2, length(dat$sellingprice)))
dat_1 %>%
ggplot(aes(x = value)) +
geom_density(fill = '#e5b9ad', color = '#e5b9ad', alpha = .5) +
geom_density(data = dat, aes(x = sellingprice), fill = 'lightgreen', color = 'skyblue', alpha = 0.4) +
labs(x = 'Значения', y = '',
title = 'Линейная модель и функции плотности') +
theme_minimal(base_family = 'Yeseva One') +
theme(plot.title = element_text(size = 14, hjust = 0.5),
plot.subtitle = element_text(size = 15),
axis.text = element_text(size = 13),
axis.title = element_text(size = 13),
axis.ticks = element_blank(),
panel.background = element_blank()) +
guides(fill = 'none') +
ease_aes('linear') +
transition_time(variable)
Как найти \(\beta_1\) и \(\beta_2\)?
Мы хотим получить оценки \(\hat{\beta_1}\) и \(\hat{\beta_2}\), которые давали бы хорошие оценки реальных цен, исходя из данных о пробеге.
Что значит хорошо? Мы хотим, чтобы оценка \(\hat{price_i}\) была как можно ближе к наблюдаемому значению \(price_i\) для всех наблюдений \(i\). Желание понятное, но вот как его добиться - не очень ясно. Давайте попробуем формализовать. Мы хотим, чтобы расстояние от точек, которые мы спрогнозировали на основании модели, до точек, отражающих реальные данные, было как можно меньшим. Т.е. \[|price_i - \hat{price_i}|\] - было как можно меньшим для всех наблюдений \(i\). Подставим формулу нашей модели: \(\hat{price_i} = \hat{\beta_0} + \hat{\beta_1} o_i\) вместо \(\hat{price_i}\) и подберём такие \(\hat{\beta_1},\hat{\beta_2}\), чтобы сумма расстояний между оценками и реальными значениями была минимальной: \[\min_{\hat{\beta_0}\hat{\beta_1}}\sum_i{|price_i - (\hat{\beta_0} + \hat{\beta_1} o_i)|}\]
Проблема в том, что данная задача выглядит просто но не решается аналитически. Поэтому исторически статистики пришли к тому, что можно немного изменить задачу при всё тех же предпосылках.
Наша задача - построить такую линию (в многомерноом случае - плоскость), чтобы сумма квадратов расстояний от каждой точки до линии (плоскости) была минимальной среди возможных. Метод, с помощью которого решается такая задача, называется методом наименьших квадратов. Чтобы получить дополнительную интуицию, советую прочитать о выводе коэффициентов в случае парной регрессии в любом из учебников, которые я рекомендовал или здесь. В лекции я приведу более общий случай с \(k\) регрессорами, в котором задача решается методами линейной алгебры.
Сначала нужно оговориться об ограничениях нашей первой модели. Оценивая МНК модель, мы пользуемся аксиомой о независимости наблюдений:
Определение:
Для двух случайных наблюдений \(i\) и \(j\) в выборке т.ч. \(i \neq j\), комбинации \((Y_i, X_i)\) независимы от \((Y_j, X_j)\). Это значит, что математическое ожидание \[ \begin{aligned} \mathbb{E}(Y_i, X_i | Y_j = y, X_j = x) &= \mathbb{E}(Y_i, X_i) \end{aligned} \]
МНК
У нас есть табличка с \(n\) наблюдениями и \(k\) регрессорами.
\[ (Y,X) = \begin{pmatrix} Y_1 & X^1_1 & \cdots & X^k_1 \\\\ \vdots & \vdots &\ddots & \vdots \\\\ Y_n & X^1_n & \cdots & X^k_n \end{pmatrix} \]
Тогда наша модель выглядит:
\[ \begin{pmatrix} Y_1 \\\\ Y_2 \\\\ \vdots \\\\ Y_n \end{pmatrix} = \begin{pmatrix} X^1_1 & \cdots & X^k_1 \\\\ X^1_2 & \cdots & X^k_2 \\\\ \vdots & \ddots & \vdots \\\\ X^1_n & \cdots & X^k_n \end{pmatrix} \begin{pmatrix} \beta_1 \\\\ \beta_2 \\\\ \vdots \\\\ \beta_k \end{pmatrix}+ \begin{pmatrix} e_1 \\\\ e_2 \\\\ \vdots \\\\ e_n \end{pmatrix} = X \beta + e \]
Решим оптимизационную задачу:
\[\min_{\hat{\beta}}(Y - X\hat{\beta})^2\]
Условия первого порядка:
\[ \begin{align} 0 \\\\ &= \frac{d}{d\hat{\beta}}[(Y - X\hat{\beta})^2] \\\\ &= \frac{d}{d\hat{\beta}}[Y^2 - 2\hat{\beta}'X'Y + \hat{\beta}'X'X\hat{\beta}'] \\\\ &= 0 - 2X'Y + 2X'X\hat{\beta} \end{align} \]
и
\[ 2X'Y = 2X'X\hat{\beta} \]
\[ X'Y = X'X\hat{\beta} \]
\[ \hat{\beta} = (X'X)^{-1}X'Y \]
Пример
- Мы хотим проверить, как влияет дополнительный год образования на ожидаемые заработные платы.
- Выборка: данные о заработных платах и образовании (в годах) по 20 индивидам.
wage = c(37.93, 40.87, 14.18, 16.83, 33.17, 29.81, 54.62, 43.08, 14.42,
14.90, 21.63, 11.09, 10.00, 31.73, 11.06, 18.75, 27.35, 24.04,
36.06, 23.08)
education = c(18, 18, 13, 16, 16, 18, 16, 18, 12, 16, 18, 16, 13, 14, 12, 16,
14, 16, 18, 16)
lwage = log(wage)
X <- matrix(c(education, rep(1, 20)), ncol = 2, nrow = 20) # 20x2 матрица
p1 <- MASS::ginv(t(X) %*% X) # (X'X)^(-1)
p2 <- t(X) %*% lwage # X'Y
betas <- p1 %*% p2
example <- c(12, 1) # Ожидаемая заработная плата индивида, проучившегося 12 лет.
y_hat <- X %*% betas # Оценки Y
e_hat <- lwage - y_hat # ОшибкиЗадание
Покажите, что квадраты ошибок
e_hatне зависят (или зависят) от наблюденийX.
Определение
Гомоскедастичной является модель, для которой верно \(\mathbb{E}[e|X_i] = \mathbb{E}[e|X_j]\) для всех наблюдений \(i,j\).
В метод, которым мы оцениваем нашу регрессионную модель одновременно заложены и feature и bug. МНК предполагает, что:
\[ \begin{align} \mathbb{E}(X'e) \\\\ &= \mathbb{E}[X'(Y - X\beta)] \\\\ &= \mathbb{E}[X'Y - X'X(X'X)^{-1}X'Y] \\\\ &= \mathbb{E}[X'Y - X'Y] \\\\ &= 0 \\\\ &= \mathbb{E}[e] \end{align} \]
И если так совпали звёзды, что \(e\) не зависит от \(X\), то
\[ \mathbb{E(X'e)^2} = \mathbb{E}(e^2) = \sigma^2 \]
и наши оценки \(\hat{\beta}\) имеют хорошие свойства из учебника, которые мы обсудим дальше.
Вопрос.
Каким образом это предположение может быть нарушено для нашего примера?
Авторы более старых учебников объясняют гомоскедастичность, как свойство хорошо специфицированной модели, а гетероскедастичность у них считается отклонением от нормы. Такое объяснение повлияло на поколения экономистов, но на практике всё, как правило, наоборот. Экономическим моделям присуща гетероскедастичность, а то время как гомоскедастичность - необычное, крайне редко встречающееся свойство. В эмпирике полезно подразумевать, что ошибки гетероскедастичны, не гомоскедастичны.
Определение
Несмещённой называется оценка \(\hat{\theta}\), для которой \(\mathbb{E}[\theta] = \hat{\theta}\).
Докажем, что оценки МНК несмещённые. Наша модель описывается двумя уравнениями: \[ \mathbb{E}[Y|X] = \begin{pmatrix} \vdots \\\\ \mathbb{E}[Y_i|X] \\\\ \vdots \end{pmatrix} = \begin{pmatrix} \vdots \\\\ X_i\beta \\\\ \vdots \end{pmatrix} = X\beta \] и \[ \mathbb{E}[e|X] = \begin{pmatrix} \vdots \\\\ \mathbb{E}[e_i|X] \\\\ \vdots \end{pmatrix} = \begin{pmatrix} \vdots \\\\ \mathbb{E}[e_i|X_i] \\\\ \vdots \end{pmatrix} = 0 \]
Мы помним, что \(\hat{\beta} = (X'X)^{-1}X'Y\). Тогда:
\[ \begin{align} \mathbb{E}[\hat{\beta}|X] \\\\ &=(X'X)^{-1}X'\mathbb{E}[Y|X] \\\\ &=(X'X)^{-1}X'X\beta \\\\ &=\beta \end{align} \]
ч.т.д.
Примечание:
Чтобы оценка МНК Была несмещённой, необходимо, чтобы наблюдения были независимы и одинаково распределены.
Примеры смещённых и несмещённых оценок с графиками.
Теорема Гаусса-Маркова
Оценки МНК - BLUE (best linear unbiased estimators), лучшие линейные несмещённые оценки. Оценка МНК имеет наименьшую дисперсию среди всех несмещённых оценок. Иными словами, в модели: \[Y = X\beta + e\] \[\mathbb{E}[e|X] = 0\] \[var[e|X] = I_n\sigma^2\] Если \(\hat{\beta}\) - несмещённая оценка для \(\beta\), то: \[var[\hat{\beta}] \geq \sigma^2(X'X)^{-1}\]
Утверждение
Ошибки в модели, оценённой МНК, имеют нормальное распределение.
Торговля подержанными автомобилями: продолжение
Call:
lm(formula = log(data$sellingprice) ~ log(data$odometer))
Residuals:
Min 1Q Median 3Q Max
-7.3657 -0.0520 0.1613 0.2903 1.6081
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 13.292588 0.063743 208.53 <2e-16 ***
log(data$odometer) -0.408809 0.006041 -67.68 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.5562 on 10390 degrees of freedom
(2 пропущенных наблюдений удалены)
Multiple R-squared: 0.3059, Adjusted R-squared: 0.3059
F-statistic: 4580 on 1 and 10390 DF, p-value: < 2.2e-16Посмотрим на распределение остатков.
Warning: `data_frame()` was deprecated in tibble 1.1.0.
ℹ Please use `tibble()` instead.df %>%
ggplot(aes(x = e)) +
geom_density(fill = '#e5b9ad', color = '#e5b9ad', alpha = .5) +
geom_vline(xintercept = mean(df$e), color = 'brown', alpha = 0.5, linetype = 'dashed') +
labs(x = 'Значения', y = '',
title = 'Распределение остатков в модели') +
theme_minimal(base_family = 'Yeseva One') +
theme(plot.title = element_text(size = 15, hjust = 0.5),
plot.subtitle = element_text(size = 15),
axis.text = element_text(size = 13),
axis.title = element_text(size = 14),
axis.ticks = element_blank(),
panel.background = element_blank()) +
scale_x_continuous(limits = c(-3,2)) +
guides(fill = 'none')Warning: Removed 21 rows containing non-finite outside the scale range
(`stat_density()`).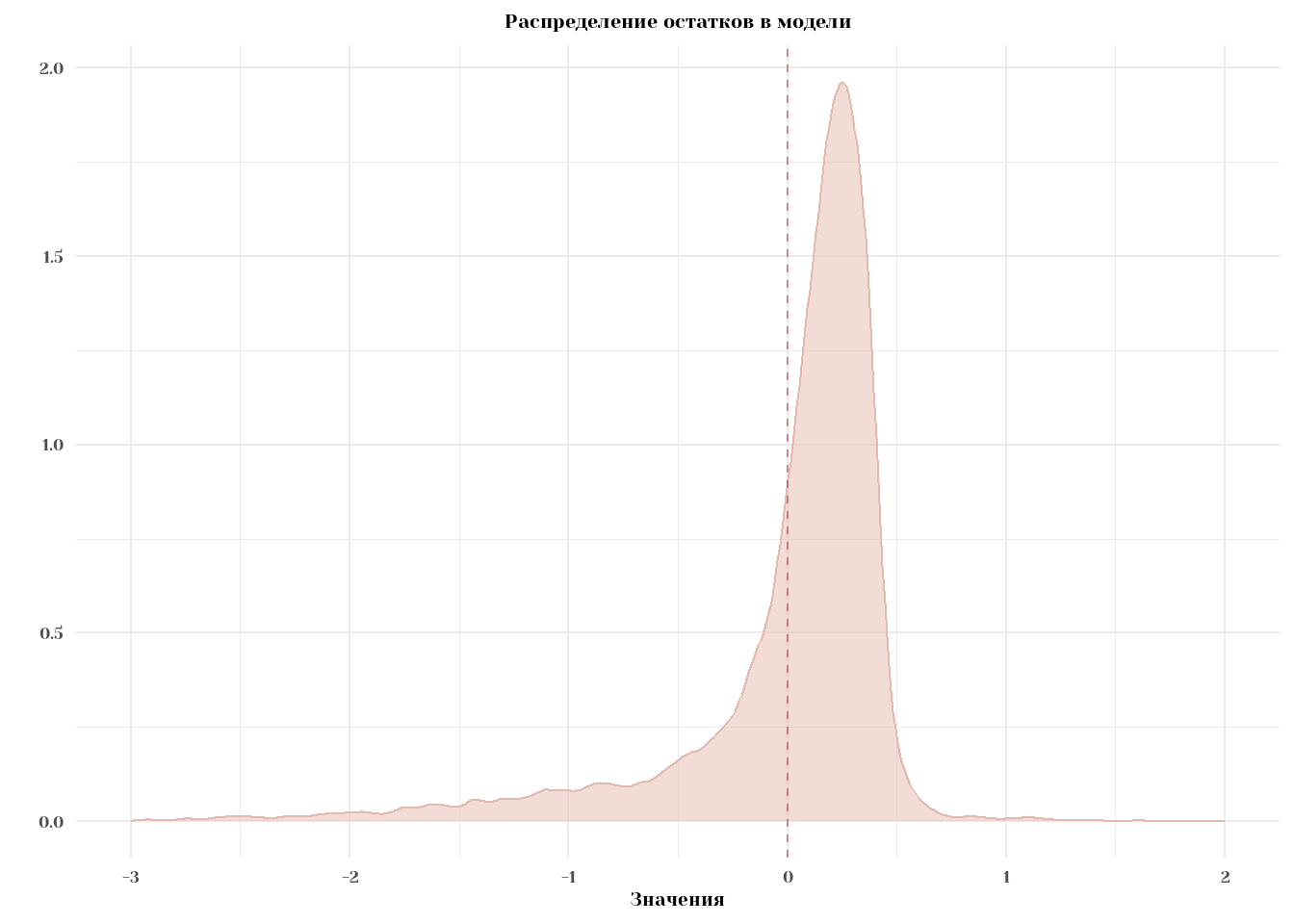
Действительно, по построению \(\mathbb{E}[e] = 0\) и cor(x, e) = 0. Распределение, конечно, выглядит так себе, но вроде бы пойдёт.
Построим такой же график для распределения e^2:
df %>%
ggplot(aes(x = e^2)) +
geom_density(fill = '#e5b9ad', color = '#e5b9ad', alpha = .5) +
geom_vline(xintercept = mean(df$e^2), color = 'brown', alpha = 0.5, linetype = 'dashed') +
labs(x = 'Значения', y = '',
title = 'Распределение квадратов остатков в модели') +
theme_minimal(base_family = 'Yeseva One') +
theme(plot.title = element_text(size = 15, hjust = 0.5),
plot.subtitle = element_text(size = 15),
axis.text = element_text(size = 13),
axis.title = element_text(size = 14),
axis.ticks = element_blank(),
panel.background = element_blank()) +
scale_x_continuous(limits = c(-0.1,1.5)) +
guides(fill = 'none')Warning: Removed 461 rows containing non-finite outside the scale range
(`stat_density()`).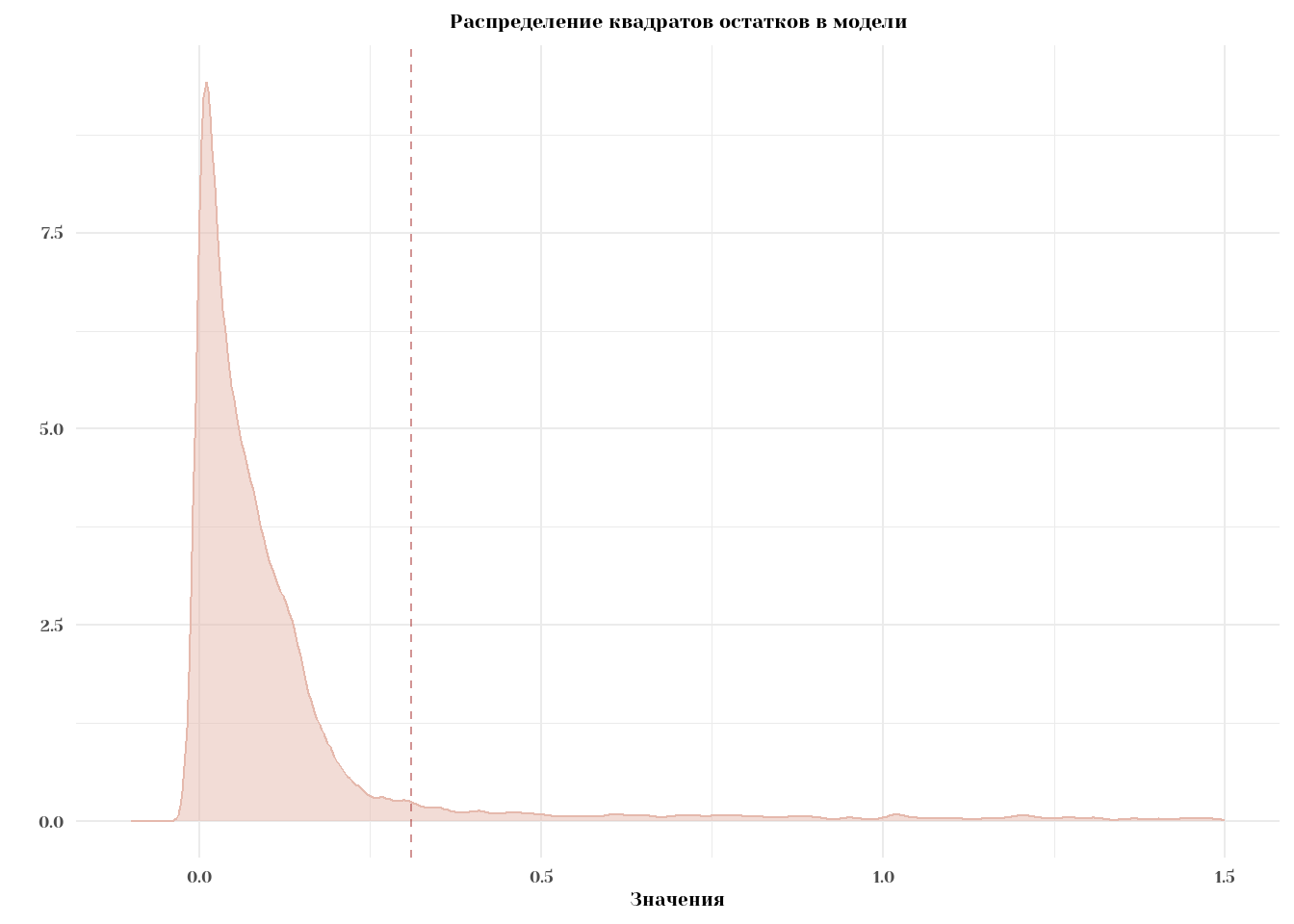
Вопрос
Какое распределение имеет \(\sigma^2\)?
Определение
Случайная величина \(X\) имеет стандартное нормальное распределение, записывается \(X \sim N(0,1)\), если её функция плотности: \[\phi(x) = \frac{1}{\sqrt{2\pi}}\exp(-\frac{x^2}{2})\]
Нарисовать функцию плотности и функцию распределения.
Теорема
Если \(X \sim N(\mu, \sigma)\) и \(Y = a+ bX\), то \(Y \sim N(a + b\mu, b^2\sigma)\).
Следствие
Пусть мы оценили обыкновенную линейную модель: \[Y = X'\beta + e\], В которой все \((Y, X)\) распределены нормаьно, а \(X\) независимы. Тогда: \(\mathbb{E}[e|X] = E[e] = 0\) (следует из независимости \(e\) от \(X\)), а \(\mathbb{E}[e^2|X] = \mathbb{E}[e^2] = \sigma^2\). Следовательно, модель гомоскедастична.
Утверждение
В регрессионной модели, где \((Y,X)\) нормально распределены: \[\hat{\beta}|X \sim N(\beta, \sigma^2(X'X)^{-1})\]
Утверждение
В регрессионной модели, где \(Y|X \sim N(\mu, \sigma^2)\) нормально распределены: \[\hat{\beta}|X \sim N(\beta, \sigma^2(X'X)^{-1})\] Это более слабое утверждение. например, \(X_i\) может быть распределён равномерно, но сумма \(X\beta\) распределена нормально.
Определение
Пусть \(X_i \sim N(0,1)\) для \(i = 1:k\), тогда: X_1 + X_2 +… +X_k ^2_k. Иными словами, сумма k стандартных нормальных случайных величин имеет хи-квадрат распределение с k степенями свободы.
Утверждение
В модели, в которой \(Y|X \sim N(\mu, \sigma^2)\), выборочная дисперсия имеет \(\chi^2\) распределение, а именно: \[\frac{(n-k)s^2}{\sigma^2} \sim \chi^2_{n-k}\]
Последнее утверждение может показаться сложным и запутанным, но на самом деле, в нём достаточно просто разобраться. В нашем предположении \(Y \sim N\), \(Y\) следует какому-то нормальному распределению. То же самое верно и для оценённых значений \(Y\), \(\hat{Y}|X \sim N\) - они тоже распределены нормально. Дисперсия в регрессии, по определению, равна: \[(Y - \hat{Y}|X)^2\] Раскрыв скобки мы получим сумму каких-то нормально распределённых случайных величин. По определению \(\chi^2\) распределения (сумма стандартных нормальных случайных величин) - мы какое-то афинное преобразовавние \(\chi^2\) распределения.
Давайте на него посмотрим:
