Лекция 1

Эконометрика

Автор

Е. Тымченко

Дата публикации

23 апреля 2023 г.

library(tidyverse)
library(scales)
library(hrbrthemes)
library(sysfonts)
library(showtext)
library(fitdistrplus)
library(haven)
library(reshape2)
library(magrittr)
library(rcartocolor)

showtext.auto()
font_add_google('Lobster')
font_add_google('Pacifico')

Тема:

Вероятности, распределения.
Независимость.
Условные вероятности, условные распределения.
ЦПТ и ЗБЧ.
Бутстрап.
Кейс: школьный эксперимент.

Вероятности и распределения.

Вероятностное пространство: \(\{\Omega, \mathcal{F}, \mathbb{P}\}\) - в чём идея?

\(\Omega\) - элементарные события.
\(\mathcal{F}\) - \(\sigma\)-алгебра на \(\Omega\).
\(\mathbb{P}\) - отображение \(\mathcal{F}\) в \([0,1]\).

Зачем это всё нужно? Так проще не запутаться и измерить в итоге то, что нужно. Самый простой пример - подкидывание кубика:

Элементарные события - выпал \(\Omega = \{1,2,3,4,5,6\}\)
1, “выпал число 1”, - алгебра. Значит, \(\bar{1}\) “1 не выпало” - тоже алгебра. Назовите ещё какие-нибудь алгебры.
Вероятность устанавливает соответствие между элементами из \(\mathcal{F}\) и отрезком \([0,1]\) так, что \(P\{\Omega\} = 1\), и \(P(A и B) = P(A) + P(B)\) для непересекающихся событий \(А\) и \(B\).

Условная вероятность:

Пример. Мы бросаем две игральные кости. На одной кости выпало 2. Какова вероятность, что сумма выпавших чисел больше 6? \[P(X + Y > 6 | X = 2) = P{Y \geq 5} = P(Y = 5) + P(Y = 6) = 2/6 = 1/3\]

Формально: \(P(X | Y) = \frac{P(X \cap Y)}{P(Y)}\)

Два типа сходимости, ЗБЧ и ЦПТ:

Сходимость по вероятности:

Случайная величина \(X\) сходится к числу \(X_c\) по вероятности если существует такое число \(\epsilon >0\), что \(\lim_{n -> \infty}P(|X_n - X_c| \geq \epsilon) = 0\)

Закон больших чисел использует эту идею. Вместо \(X_n\) - выборочное среднее, вместо \(X_c\) - теоретическое среднее.

Для определения вероятностей событий сведений о среднем недостаточно. Нам нужно понимать, как распределена случайная величина. С этим может помочь центральная предельная теорема.

\[\frac{(X_1 + X_2 + ... + X_n) - n \mu}{\sqrt{n}\sigma} \to^d N(0, 1)\] Чтобы она выполнялась, нужно выполнение всего трёх условий!

\(X_i\) и \(X_j\) независимы для всех \(i,j\)
Все \(X\) одинаково распределены.
\(X\) имеют конечную дисперсию.

В статистике очень много внимания уделено случаям, когда одно из этих условий не выполняется. Например, Теорема Ляпунова показывает, что \(X\) могут быть по-разному распределены. Относительно кратко и доступно об этой части теории можно почитать здесь. или в учебнике по статистике, который я советовал к курсу, Bremaud, P.

Если вы не поняли моё объяснение в классе, я очень советую посмотреть образовательное видео с роскошными визуализациями от Гранта Сандерсона

Задание

Запрограммируйте пример с доской Гальтона с параметрами \({исходы = \{1, 2,...,12\}, p = 1/2}\). Нарисуйте гистограмму получившегося распределения.

Пример 1

Знакомство с генератором случайных чисел:

purrr::rbernoulli(5, p = 0.7)

[1] FALSE  TRUE FALSE FALSE FALSE

Работает ли ЗБЧ?

dist_kisses <- function(n,p,k){ # Создадим функцию
  means <- c() # means - пустой вектор
  for (i in 1:k){ # Мы k раз
    means[i] <- rbinom(n = n, prob = p, size = i) / i %>% mean() # добавляем в вектор means долю успехов 
  } # в n испытаниях по схеме Бернулли.
  return(means) # и возвращаем вектор means с n наблюдениями
}

Давайте убедимся в ЗБЧ: посмотрим, как оценка \(\hat{p}\) стремится к истинному значению \(p = 0.7\) с ростом выборки.

n = 200
p = 0.7
k = 2000

data.frame(P = dist_kisses(n,p,k),
           K = seq(1, k, by = 1)) %>%
  mutate(mycolor = ifelse(P > 0.7, "type1", "type2")) %>%
  ggplot(aes(x = K, y = P)) +
  geom_segment(aes(x = K, xend = K, y = 0.7, yend = P, color = mycolor), size = 0.7, alpha = 0.4, show.legend = F) +
  geom_hline(yintercept = 0.7, size = 0.2, alpha = 0.3)  +
  scale_color_carto_d(palette = 'TealRose') +
  theme_minimal(base_family = 'Pacifico') +
  theme(plot.title = element_text(hjust = 0.5, size = 29),
        axis.title.x= element_text(size = 28),
        axis.title.y = element_text(size = 28),
        axis.text.x = element_text(size = 28),
        axis.text.y = element_text(size = 28),
        plot.background = element_rect(colour = 'white')
  ) +
  labs(title = 'ЗБЧ: Чем больше экспериментов - тем ближе p к истинному значению')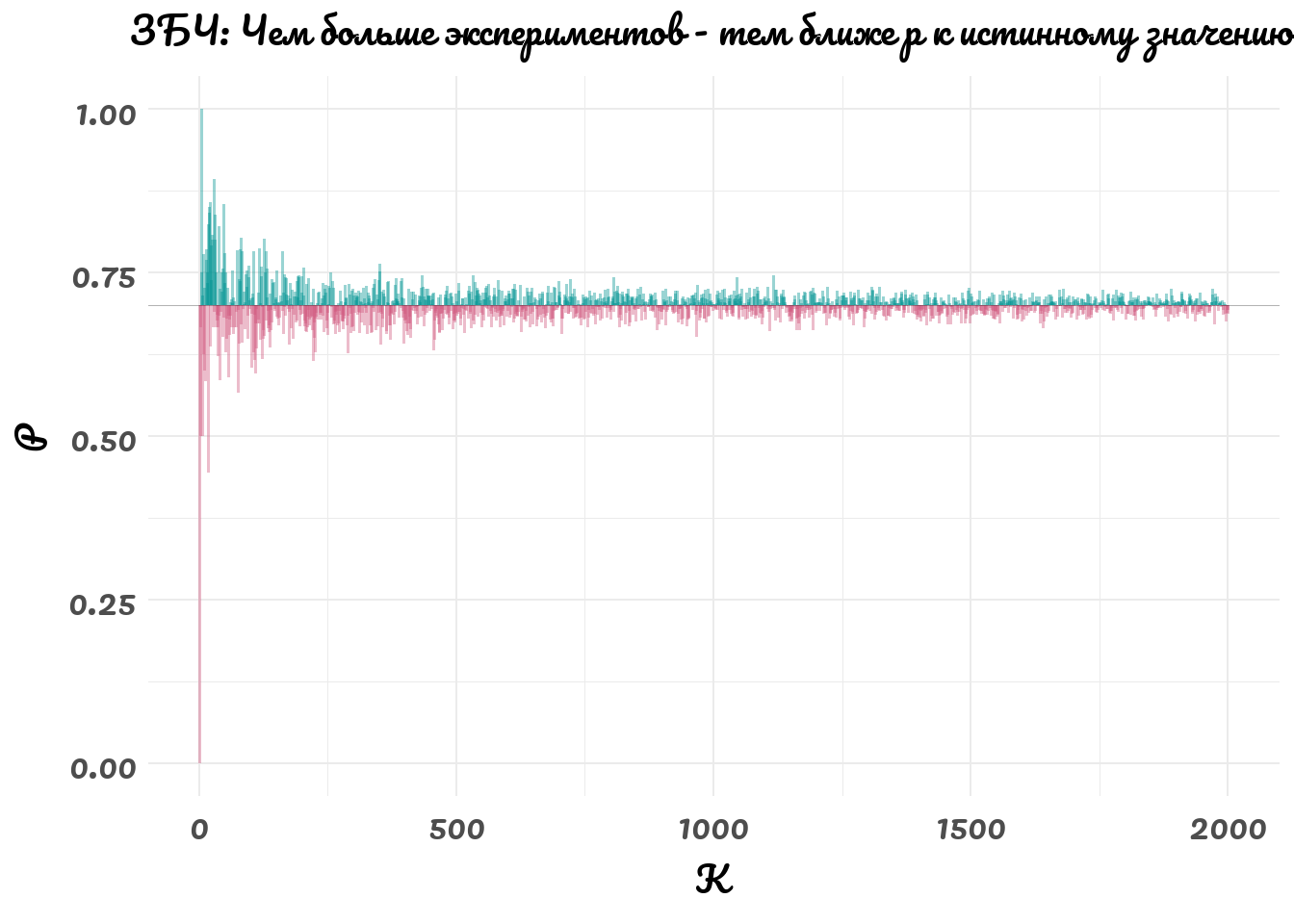

Среднее значение равно \(p\).

dist_kisses(n,p,k) %>% mean()

[1] 0.700338

Задание:

Закончите формальное доказательство ЗБЧ (сходисость по вероятности) для этого примера. Укажите произвольный \(\epsilon\), покажите, что с ростом k ошибка становится меньше \(\epsilon\).

Пример 2

Допустим, последний пример нас не убедил. Всё-таки там было очень простое распределение Бернулли, которое принимает всего 2 значения. Давайте рассмотрим пример из жизни, где исходное распределение необычное. Давайте посмотрим, как распределены доходы граждан на примере небольшой выборки:

data <- read.csv('https://raw.githubusercontent.com/ETymch/Econometrics_2023/main/Datasets/201709-CAH_PulseOfTheNation.csv')
income <- data$Income %>%
  na.omit() %>%
  as.numeric()

Посмотрим, как выглядит это распределение:

income %>% 
  data.frame %>%
  ggplot() +
    geom_histogram(mapping = aes(x = income), bins = 18,
                   col = 'skyblue',
                   fill = 'green', alpha = 0.3) +
    scale_x_continuous(breaks = breaks_width(50000)) +
    theme_minimal(base_family = 'Lobster', base_size = 19) +
    labs(x = 'Доходы', y = 'Число наблюдений', title = 'Распределение доходов в выборке')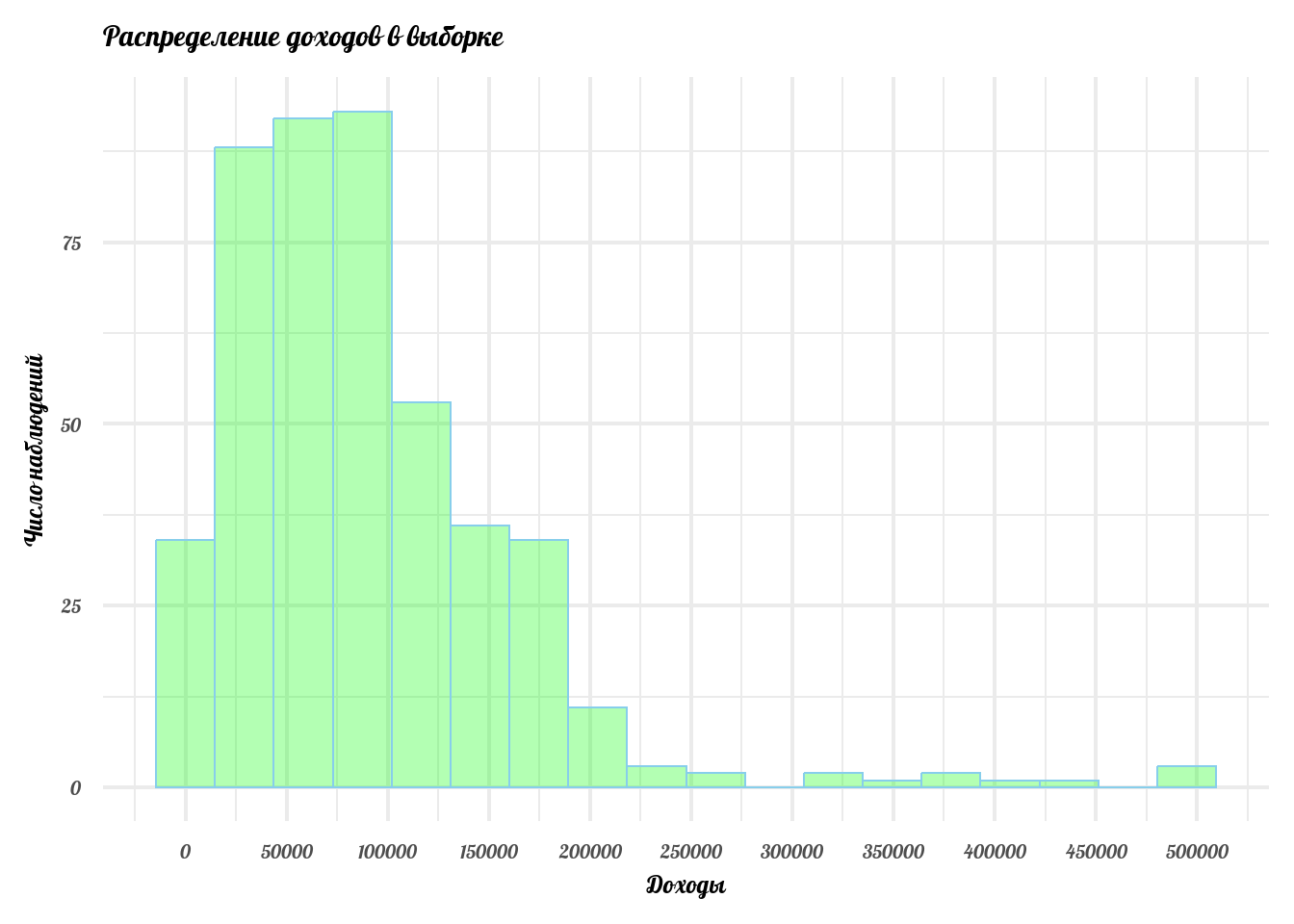

Сработает ли ЦПТ в таком случае? напишем функцию

sampling_means <- function(data, n, k){
  means <- c()
  for (i in 1:k){
    means[i] <- sample(data, n, replace = T) %>% mean # выборки с возвращением, считаем среднее k раз
  }
  means <- (means - mean(means)) / sd(means)  # приводим к стандартному нормальному распределению
  means
}

Проведём численный эксперимент:

incomes_subsamples <- sampling_means(income, 1000, 10000)
incomes_subsamples %>%
  hist(main = 'ЦПТ работает!')

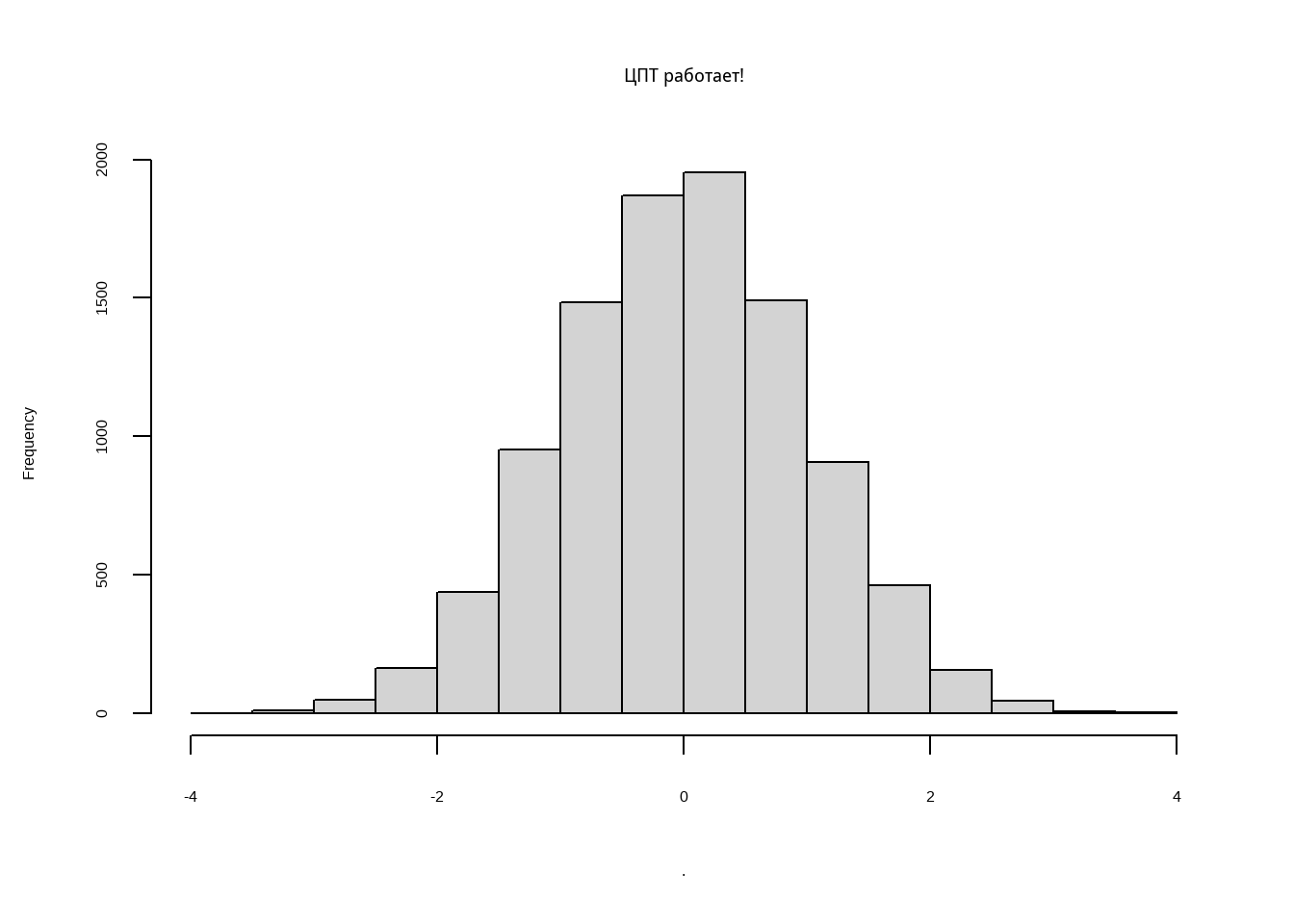
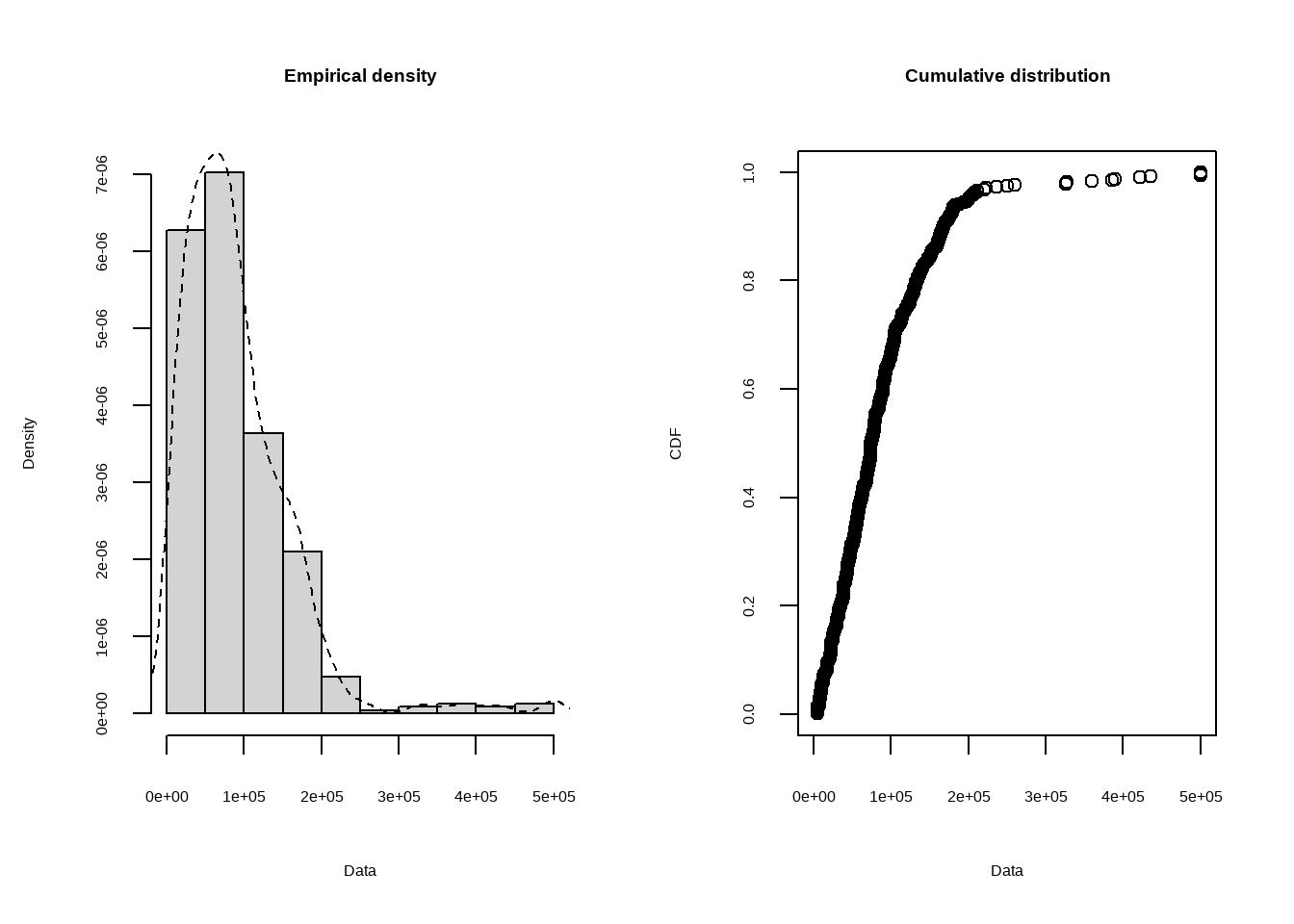
Но точно ли оно стандартное нормальное? Как узнать, может глаза нас обманывают? В R есть замечательная библиотека fitdistrplus для работы с распределениями. Давайте ещё посмотрим на функцию плотности и кумклятивную функцию распределения доходов.

fitdistrplus::plotdist(income, histo = T, demp = T)

Кумулятивная функция распределения:

\[F(x) = P(x \leq X) = \int_{-\infty}^x f(t)dt\] Функция плотности:

\[p(a \leq x \leq b) = \int_{a}^bf(x)dx\] ### Вопрос

\(f(x)\) - какое-то дискретное распределение. Какова вероятность, что \(a \leq X \leq b\) в терминах кумулятивной функции распределения?

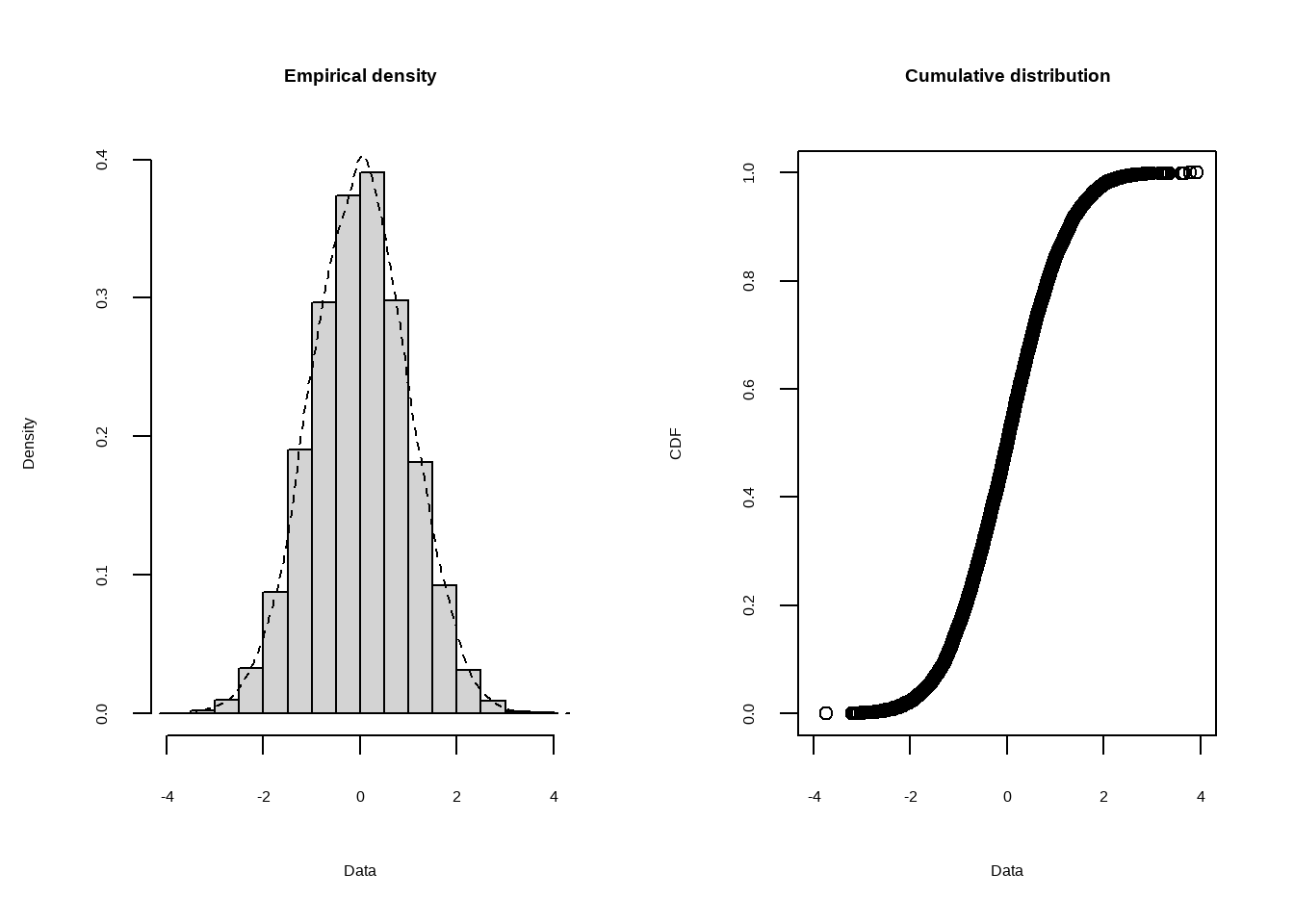
Теперь посмотрим на нормальизованное распределение:

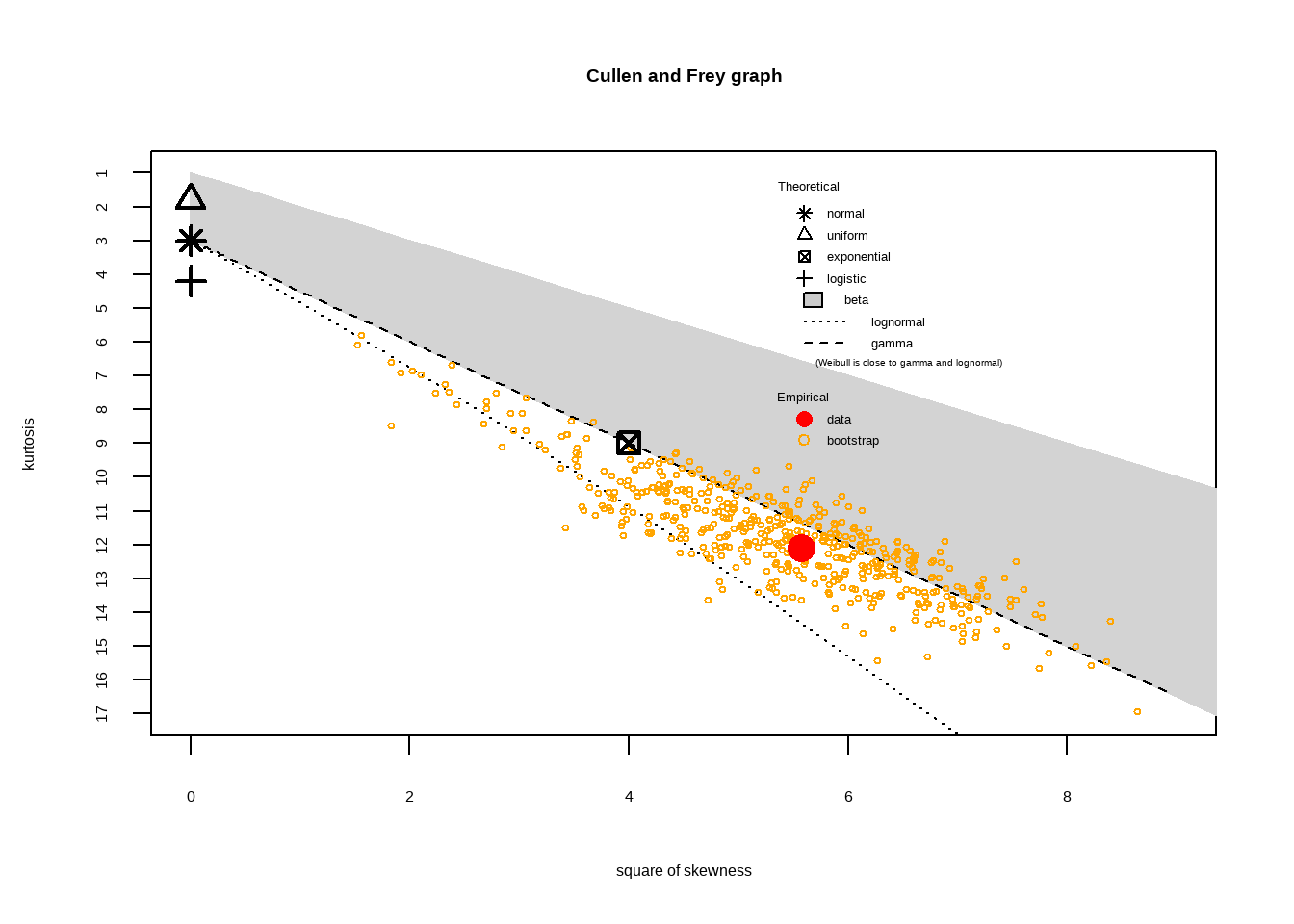
fitdistrplus::plotdist(incomes_subsamples, histo = T, demp = T)

descdist(income, discrete = F, boot = 500) # Распределение доходов похоже скорее на Гамма-распределение, чем на Логнормальное.

summary statistics
------
min:  5000   max:  5e+05 
median:  74500 
mean:  89589.91 
estimated sd:  72275 
estimated skewness:  2.359947 
estimated kurtosis:  12.09809

Распределение доходов похоже скорее на Гамма-распределение, чем на Логнормальное. Если мы немного забыли, как выглядят распределения, давайте перейдём сюда и вспомним. Теперь давайте построим график C&F для нормализованного распределения:

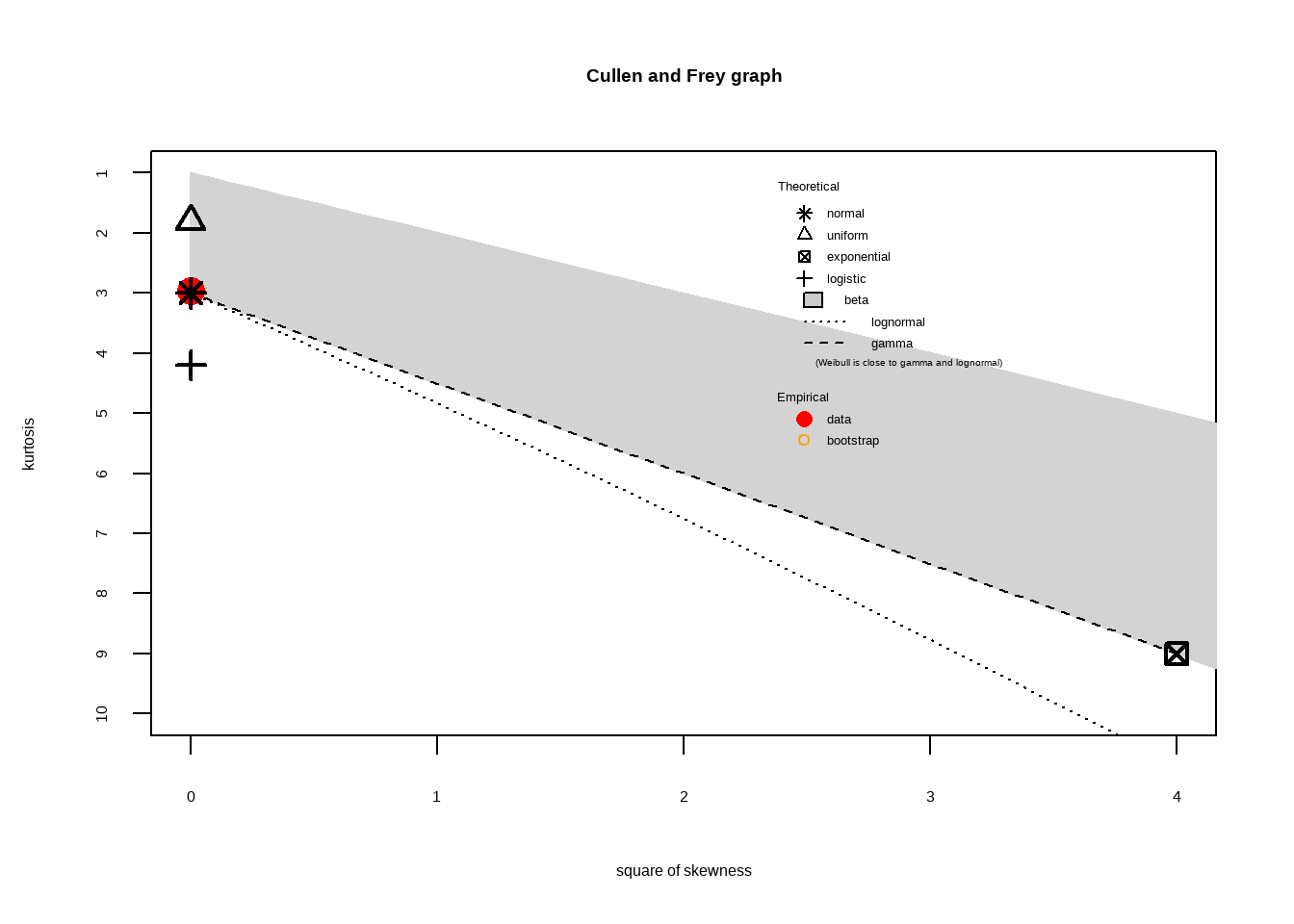
descdist(incomes_subsamples, discrete = F, boot = 500)

summary statistics
------
min:  -3.734788   max:  3.921031 
median:  0.006586643 
mean:  3.777888e-16 
estimated sd:  1 
estimated skewness:  0.008006384 
estimated kurtosis:  2.957835

Дейстаительно, наш результат - нормальное распределение с параметрами (0,1). Чтобы определить параметры распределения, воспользуемся функцией fitdist. По умолчанию она максимизирует функцию правдоподобия при условии реализовавшихся данных. Этот метод мы изучим чуть позже, пока отметим, что в нашем случае (нормальное распределение) идея в следующем:

\[\max_{\mu,\sigma} N(\mu,\sigma | данные)\]

fit_normal <- fitdist(incomes_subsamples, 'norm')
fit_normal %>% summary()

Fitting of the distribution ' norm ' by maximum likelihood 
Parameters : 
         estimate  Std. Error
mean 3.777888e-16 0.009999500
sd   9.999500e-01 0.007070682
Loglikelihood:  -14188.89   AIC:  28381.77   BIC:  28396.19 
Correlation matrix:
     mean sd
mean    1  0
sd      0  1

Вопрос

\(Z\) имеет стандартное нормальное распределение. Какова вероятность, что * \(-1 \leq Z \leq 1\), * \(Z > 2\)?

Задание

Определите распределение исходных данных о доходах. Определите параметры этого распределения. Насколько хорошо теоретическое распределение описывает данные? Воспользуйтесь тестом Колмогорова-Смирнова.

Перве знакомство с бутстрапом. Бутстраповский доверительный интервал.

bootdist(fit_normal) %>%
  summary(niter = 500) # 500 подвыборок с возвращением. Для каждой подвыборки счиатем статистику

Parametric bootstrap medians and 95% percentile CI 
           Median        2.5%      97.5%
mean 0.0001151759 -0.01981404 0.01882909
sd   0.9995112660  0.98469175 1.01373625

500 подвыборок с возвращением. Для каждой подвыборки счиатем статистику среднего и стандартного отклонения, получаем доваерительные интервалы.

Задание на повторение

Пусть \(X_1,X_2,...,X_n\) - независимые одинаоково распределённые случайные величины с дисперсией 2, \(\bar{X}\) - среднее в \(X_1,...,X_n\). Чему равно среднее квадратическое отклонение \(\bar{X}\)? Напишите код или решите аналитичсески исходя из свойств дисперсии независимых величин.

Кейс: так ли сильно наши успехи зависят от окружения?

В стетье авторы проводят интересный эксперимент. Они измеряют, как соседство по классу влияет на успеваемость. В нём часть плохо успевающих учеников начальных классов китайской школы случайным образом пеерсадили к хорошо успевающим детям. Как результат, их успеваемость повысилась.

Загрузите датасет, посмотрите, насколько много данных собрали исследователи для эксперимента. Часто, чтобы отделить treatment effect, нам нужно учесть все остальные факторы, которые могли бы влиять на успеваемость. Поэтому в датасете присутствуют данные о том, болел ли ребёнок, сколько часов в день, читал книжки и сколько занимался думскроллингом.

Сегодня мы немного в упрощённом виде повторим результат авторов. Мы ещё не умеем строить многомерные модели, чтобы определять причинно-следственные связи. Выгрузим часть данных:

data <- read_dta('https://github.com/ETymch/Econometrics_2023/blob/main/Datasets/final.dta?raw=true') %>%
  dplyr::select(math1, math2, math3, treat1, treat2) %>% # math - результат за 1,2,3 тест по математике. treat1 - ученика пересадили, но не подкрепляли дополнительными поощрениями за хорошую учёбу.
# treat2 - ученика пересадили и вознаграждали за успехи дополнительно.
  mutate(growth_end = math3 - math1, # создадим переменную, которая показывает рост/падение результатов ученика между 1 и 3 экзаменами.
         growth_mid = math2 - math1)

Посмотрим, как распределены оценки за 3 теста:

data %>% dplyr::select(math1, math2, math3) %>%
  set_colnames(c('Тест 1', 'Тест 2', 'Тест 3')) %>%
  melt %>%
  ggplot(aes(x = value, fill = variable, color = variable)) +
  geom_density(alpha = 0.6) +
  theme_minimal(base_family = 'Lobster', base_size = 25) +
  scale_fill_carto_d(palette = 'Safe') +
  scale_color_carto_d(palette = 'Safe') +
  theme(plot.title = element_text(hjust = 0.5, face = 'bold'),
        legend.title = element_blank()) +
  labs(title = 'Распределение оценок за тесты',
       x = 'Оценка', y = 'Плотность')

No id variables; using all as measure variables

Warning: attributes are not identical across measure variables; they will be
dropped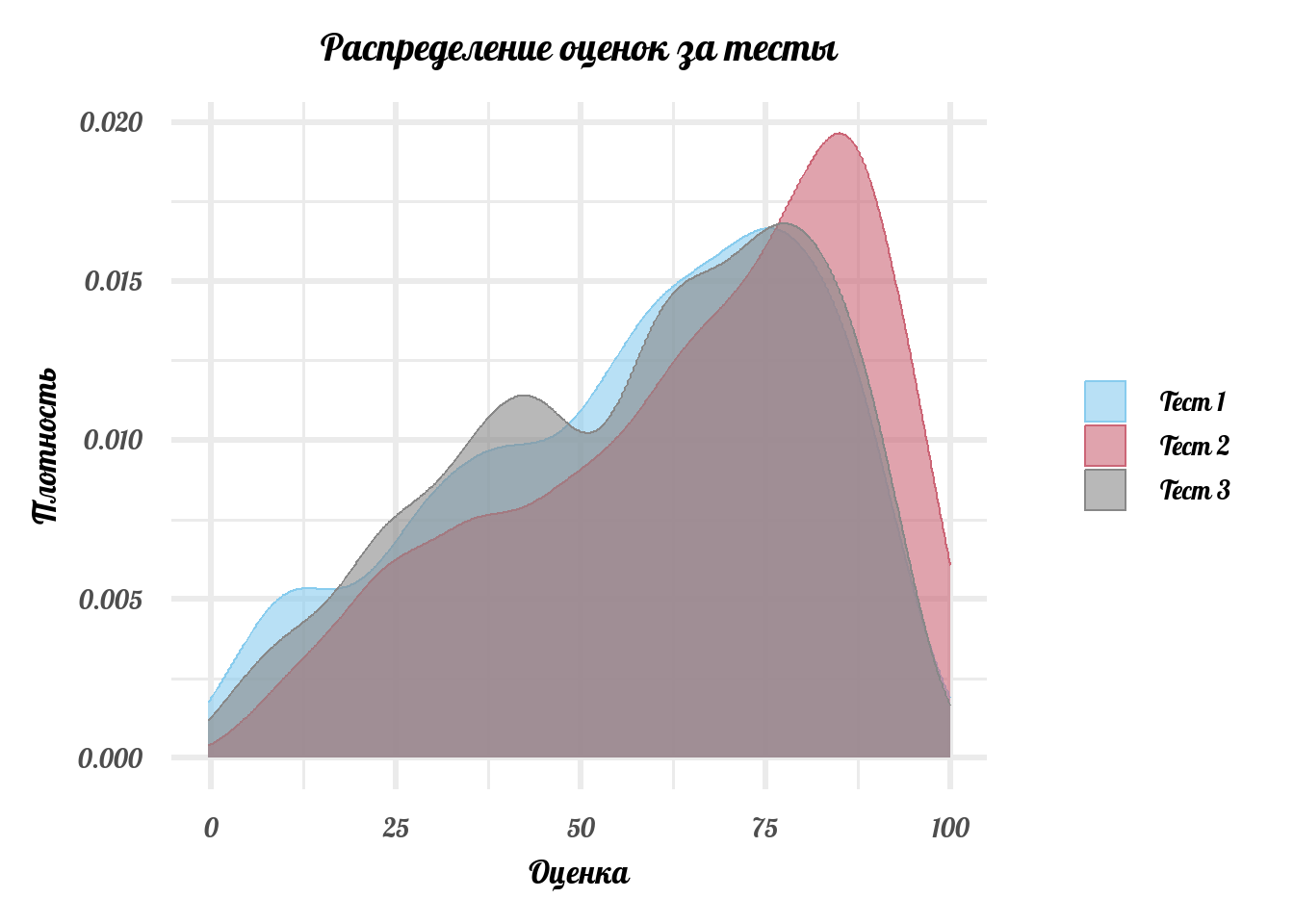

Если treatment не оказывает никакого действия, то распределение оценок без treatment-а и распределение оценок, когда мы каким-то образом воздействовали на учеников выглядят одинаково. Следовательно, среднее этих распределений тоже будет одинаковым. Проверим это. Давайте посмотрим, есть ли вообще разница в результатах между treatment и контрольной группой:

treatment <- data %>%
  filter(treat1 + treat2 >= 1)
notreatment <- data %>%
  filter(treat1 + treat2 == 0)

mean(treatment$growth_end) - mean(notreatment$growth_end)

[1] 1.616996

Как мы видим, есть небольшая разница, 1.6 балла. Достаточно ли она большая, чтобы мы могли заключить, что наш treatment как-то повлиял на успеваемость? Как это проверить?

В данном случае можно воспользоваться простой и красивой идеей - random premutation test

random_permutation <- function(data, n, k){
  m_diff <- c()
  for (i in 1:k){
  sample <- sample_n(data, n)
  sample_c <- data %>% setdiff(sample)
  m_diff[i] <- mean(sample[['growth_end']]) - mean(sample_c[['growth_end']])
  }
  m_diff
}

rp_result <- random_permutation(data, 1200, 1000)

Нарисуем результат:

data.frame(rp_result = rp_result) %>%
  ggplot(aes(x = rp_result)) +
  geom_density(alpha = 0.6, fill = '#e5b9ad', color = '#e5b9ad', size = 2) +
  theme_minimal(base_family = 'Pacifico', base_size = 25) +
  geom_vline(xintercept = mean(treatment$growth_end) - mean(notreatment$growth_end), col = 'lightgreen', alpha = 0.5, size = 2)+
  labs(title = 'Результаты теста',
       x = 'Разница в результатах между финальным и первым тестом',
       y = 'Плотность')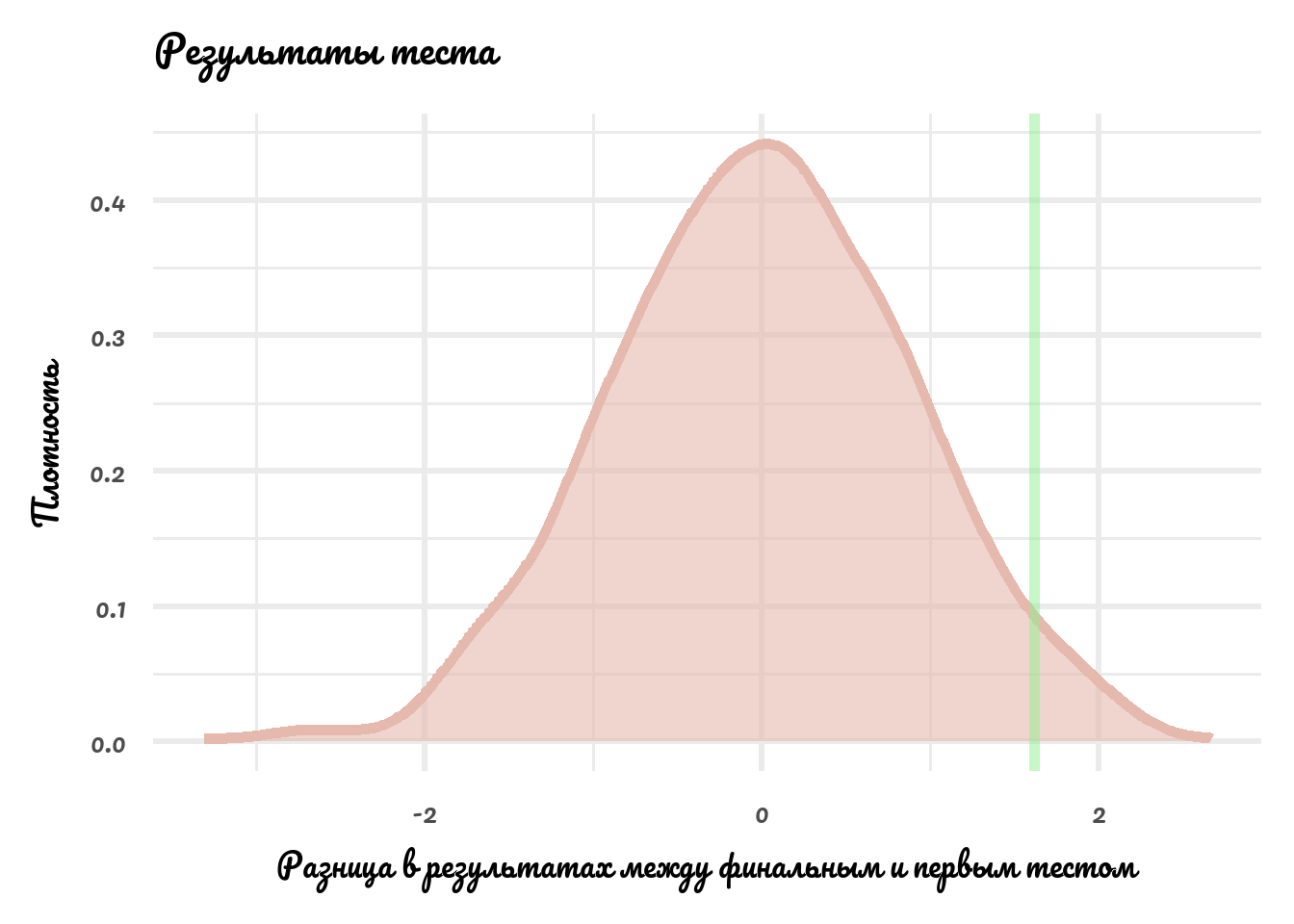

Искомое значение - интеграл функции плотности правее зелёной вертикальной линии. Или просто:

sum(rp_result > mean(treatment$growth_end) - mean(notreatment$growth_end)) / 1000

[1] 0.035

Значим ли такой результат?

Задание

Проведите rpt для разницы в результатах между вторым и первым тестом. Важно ли всегда пользоваться ЦПТ или зачастую она нужна просто для удобства?

Задание

Проводятся выборы президента. Мы знаем, что за кандидата Васю готовы проголосовать 40% населения. Допустим, мы проводим уличный опрос среди 500 случайных прохожих. Какова вероятность, что 400 из них не готовы проголосовать за Васю? Решите аналитически (используйте ЦПТ). Решите численными методами.