library(mFilter) # фильтры
library(tidyverse) # Обработка данных
library(sysfonts) # Загрузка шрифтов в R
library(showtext) # Рендер шрифтов на графиках
library(MARSS) # Многомерные модели пространства состояний
library(patchwork) # Комбинирование графиков
showtext.auto() # автоматически использовать showtext в ggplot
font_add_google('Merriweather') # Загрузка шрифта из google fonts
data <- read.csv('econ_macro_data.csv')Лекция 8
Загрузим библиотеки:
Фильтр Калмана
Допустим, у нас есть какая-то модель пространства состояний:
\[ \begin{align} &x_t = G_tx_{t-1} + w_t, \space \space w_t \sim \mathcal{N}(0, W_t) \\ &y_t = F_tx_t + v_t, \space \space \space \space \space \space \space \space v_t \sim \mathcal{N}(0, V_t) \\ &x_0 \sim \mathcal{N}(m_0, C_0) \end{align} \] Где первое уравнение описывает переход между различными состояниями системы. Второе - описывает то, как различные состояния соотносятся с наблюдаемыми нами данными. Третье уравнение описывает начальные условия.
Фильтр Калмана - оптимальный способ получения ненаблюдаемых состояний из такой системы. Это очень важный для понимания алгоритм. Давайте посмотрим на него:
- Сначала мы получаем фильтрационное распределение \(x_{t-1}\). Оно у нас всегда есть и для нулевого периода оно задано, поэтому здесь проблем никаких нет. \(x_0 \sim \mathcal{N}(m_0, C_0)\).
- Далее из распределения \(x_0\) мы хотим получить распределение \(x_1\). Это делается по следующей схеме:
- Мы получаем распределение прогноза на шаг вперёд просто подставляя распределение \(x_0\) в первое уравнение: \[ \begin{align} &a_1 = \mathcal{E} x_1 = G_t \mathbb{E}x_0 + \mathbb{E}w_0 \\ &R_1 = Var x_1 = G_1 C_0 G^T_1 + W_1 \end{align} \]
- Затем мы должны выписать функцию правдоподобия, чтобы поставить оптимизационную задачу и её решить. Функция правдоподобия описывает то, насколько хорошо наша вероятностная модель соответствует данным. То есть, распределение состояния, \(N(a_1,R_1)\) мы подставляем во второе уравнение: \[\begin{align} &f_1 = F_1 a_1 \\ &Q_1 = F_1 R_1 F^T_1 + V_t \end{align}\]
- Далее нам нужно посчитать Kalman gain. Я прошу прощения за англицизмы, будет лучше, если этот термин вы так и запомните на английском. KG - это оптимизационный коэффициент корректировки, про который подробнее расскажем далее. \[ K_1 = R_1 F^T_1 Q_1^{-1} \]
- Теперь после того, как мы получили первоначальное состояние и прогноз, увидели, что прогноз как-то отличается от значений в табличке с данными, мы можем обновить (скорректировать) текущее состояние! \[ \begin{align} &m_1 = a_1 + K_1(y_1 - f_1) \\ &C_1 = [I - K_1F_1]R_1 \end{align} \]
- Фильтрационное распределение в период 2 \(x_1 \sim \mathcal{N}(m_1, C_1)\). И так далее!
Чтобы реализовать такой алгоритм, мы можем написать простую программу:
Kalman_filtering <- function(m_t_minus_1, C_t_minus_1, t){
# Фильтрационное распределение
a_t <- G_t %*% m_t_minus_1
R_t <- G_t %*% C_t_minus_1 %*% t(G_t) + W_t
# Прогноз на шаг вперёд
f_t <- F_t %*% a_t
Q_t <- F_t %*% R_t %*% t(F_t) + V_t
#Kalman gain
K_t <- R_t %*% t(F_t) %*% solve(Q_t) # RF^TQ^-1
# Обновление состояния
m_t <- a_t + K_t %*% (y[t] - f_t)
C_t <- (diag(nrow(R_t)) - K_t %*% F_t) %*% R_t
# Возвратить список: Мат. ожидание текущего состояния; Дисперсия текущего состояния; Мат. ожидание фильтрационного распределения; Дисперсия Фильтрационного распределения
list(m = m_t, C = C_t, a = a_t, R = R_t)
}Оценим эту модель для Urals.
y <- data$Urals # искомый вектор
t_max <- length(y) # Кол-во периодов
# Параметры
G_t <- matrix(1, 1, 1)
W_t <- matrix(1, 1, 1)
F_t <- matrix(1, 1, 1)
V_t <- matrix(1, 1, 1)
m0 <- matrix(y[1], 1, 1)
C0 <- matrix(1, 1, 1)
# Создаём в памяти векторы:
m <- rep(NA, t_max)
C <- rep(NA, t_max)
a <- rep(NA, t_max)
R <- rep(NA, t_max)
# Рассчитываем состояние для первого периода:
KF <- Kalman_filtering(m0, C0, t = 1)
m[1] <- KF$m
C[1] <- KF$C
a[1] <- KF$a
R[1] <- KF$R
# Для последующие периодов:
for (t in 2:t_max){
KF <- Kalman_filtering(m[t-1], C[t-1], t = t)
m[t] <- KF$m
C[t] <- KF$C
a[t] <- KF$a
R[t] <- KF$R
}
# Сделаем график:
tibble(index = as.Date(data$Date), y, m) %>%
ggplot() +
geom_point(aes(x = index, y = y), col = 'orange', size = 2, alpha = 0.5) +
geom_line(aes(x = index, y = m), col = 'purple', size = 1.1, alpha = 0.3) +
theme_minimal(base_family = 'Merriweather') +
labs(x = 'Год')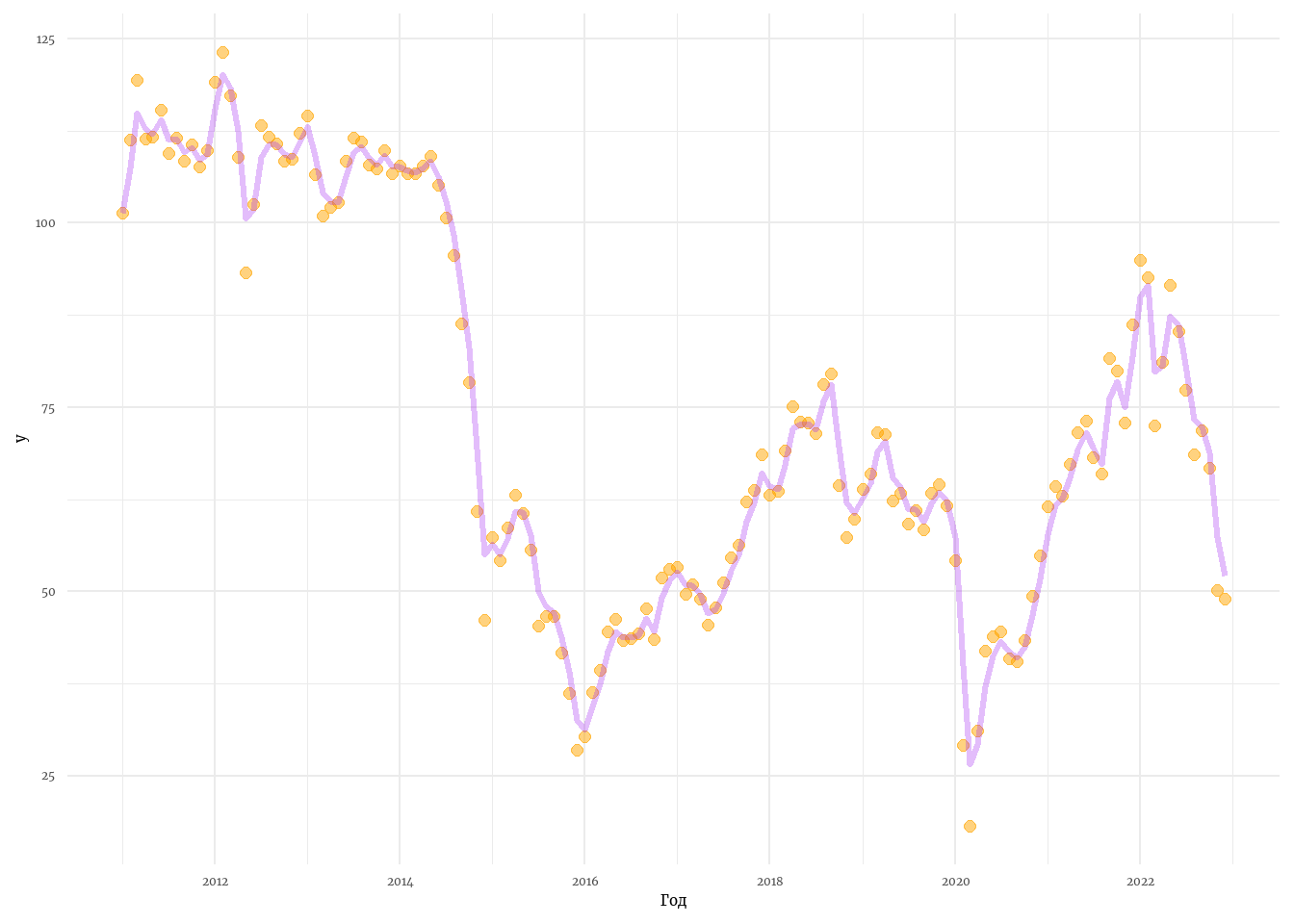
Структурные сдвиги
Как и прежде, продолжим двигаться от простого к сложному. В моделировании мы будем использовать библиотеку MARSS - на мой взгляд, для первого знакомства с моделями пространства состояний - эта библиотека держит отличный баланс между созданием общего понимания, как модели устроены, и компактностью/удобностью. Модели в MARSS устроены следующим образом:
\[ \begin{align} &x_t = B_tx_{t-1} + u_t + C_tc_t + G_tw_t, \space \space w_t \sim \mathcal{MVN}(0,Q_t) \\ &y_t = Z_tx_t + a_t + D_td_t + H_tv_t, \space \space v_t \sim \mathcal{MVN}(0, R_t) \\ &x_0 \sim \mathcal{MVN}(\pi, \Lambda) \end{align} \] Где \(x_t\) - состояния, \(y_t\) - данные, \(x_0\) - начальные условия. Лучше всего получить интуицию о том, как устрена такая модель - идти от простого к сложному, чем мы и займёмся. Рассмотрим модель с одним уровнем.
Модель неизменного уровня
Это, пожалуй, самая простая из возможных моделей. Выглядит она так (большинство членов из полной записи выше равны нулю и пропущены):
\[ \begin{align} &x_t = x_{t-1} \\ &y_t = x_t + v_t, \space \space v_t \sim \mathcal{N}(0,r) \\ &x_0 = a \end{align} \]
Т.е. в модели есть какое-то одно состояние, которое на протяжении всего периода наблюдений не меняется. При этом, данные каким-то образом распределены вокруг этого состояния.
y <- data$Urals %>% # табличка с ценами на нефть
t()
# Параметры
Z = matrix(1, 1, 1) # Это просто цифра, но подход требует, чтобы она была записана в матрицу. Первое значение - сама цифра 1, вторая - кол-во строк в матрице, третья - кол-во столбцов.
B = matrix(1, 1, 1)
A = matrix(0, 1, 1)
U = matrix(0, 1, 1)
R = matrix('r', 1, 1) # буковка значит, что этот параметр мы оцениваем при помощи ММП.
Q = matrix(0, 1, 1)
x0 = matrix('a') # буковка значит, что этот параметр мы оцениваем при помощи ММП.
model_ll <- MARSS(y, model = list(Z = Z, B = B, A = A, U = U, R = R, Q = Q, x0 = x0)) # Модель локального уровняSuccess! algorithm run for 15 iterations. abstol and log-log tests passed.
Alert: conv.test.slope.tol is 0.5.
Test with smaller values (<0.1) to ensure convergence.
MARSS fit is
Estimation method: kem
Convergence test: conv.test.slope.tol = 0.5, abstol = 0.001
Algorithm ran 15 (=minit) iterations and convergence was reached.
Log-likelihood: -675.969
AIC: 1355.938 AICc: 1356.023
Estimate
R.r 699.7
x0.a 74.1
Initial states (x0) defined at t=0
Standard errors have not been calculated.
Use MARSSparamCIs to compute CIs and bias estimates.states <- model_ll$states %>% c() # Извлекаем из модели результат - состояния
# Сделаем иллюстрацию:
tibble(Date = as.Date(data$Date),
Long_Run_state = states,
Urals = data$Urals) %>%
ggplot(aes(x = Date)) +
geom_point(aes(y = Urals), color = 'orange', alpha = 0.5) +
geom_line(aes(y = Long_Run_state), color = 'purple', size = 1.1, alpha = 0.4) +
theme_minimal(base_family = 'Merriweather') +
theme(plot.title = element_text(hjust = 0.5)) +
labs(title = 'Самая простая модель')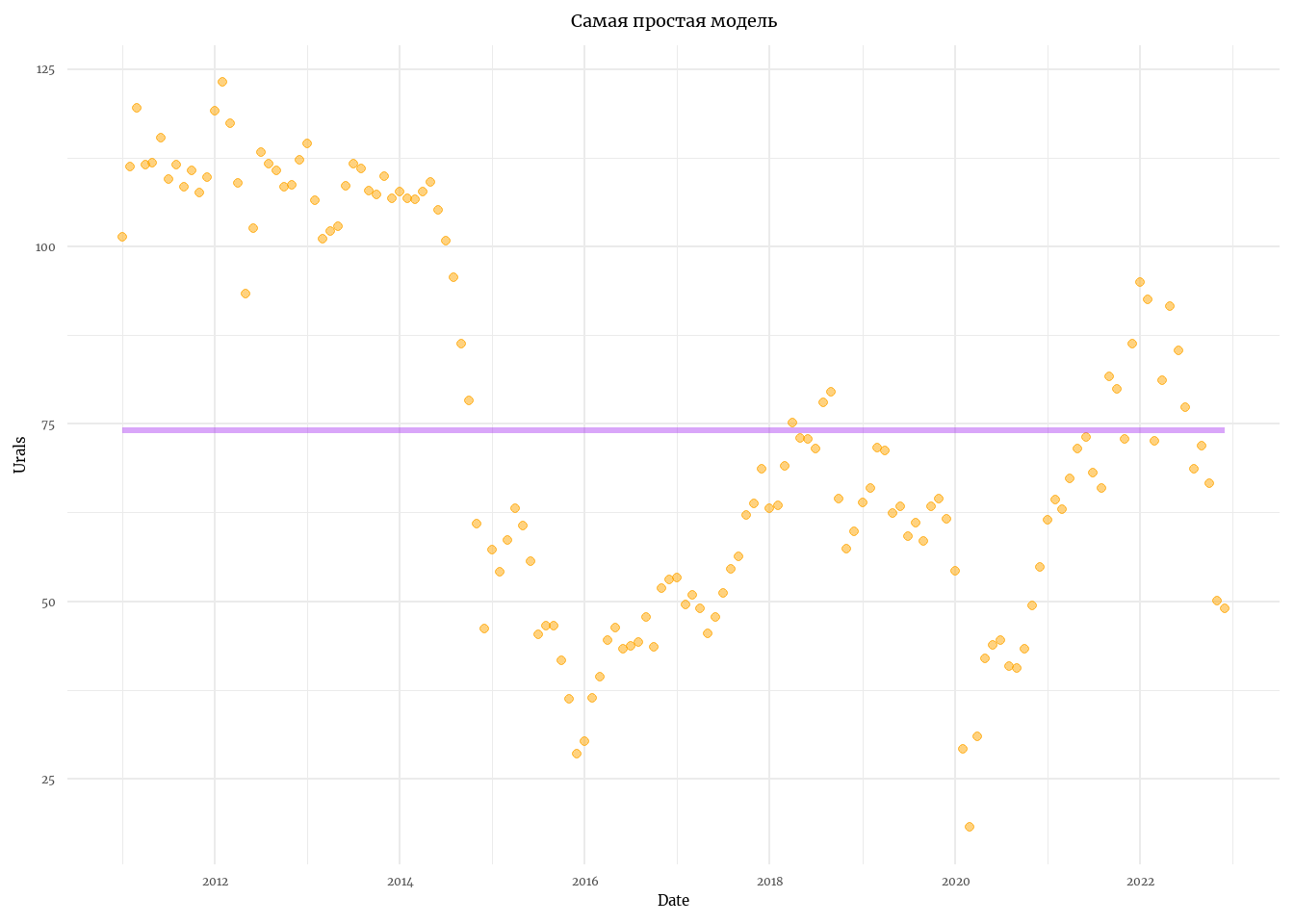
Модель меняющегося уровня
Намного интереснее предположить, что состояние в течение периода наблюдений меняется, существует некоторый линейный тренд. Заметьте, что состояние в данной модели - детерминированная величина, а данные зашумлены.
\[ \begin{align} &x_t = x_{t-1} + u\\ &y_t = x_t + v_t, \space \space v_t \sim \mathcal{N}(0,r) \\ &x_0 = a \end{align} \]
# Параметры
Z = matrix(1, 1, 1) # Это просто цифра, но подход требует, чтобы она была записана в матрицу. Первое значение - сама цифра 1, вторая - кол-во строк в матрице, третья - кол-во столбцов.
B = matrix(1, 1, 1)
A = matrix(0, 1, 1)
U = matrix('u', 1, 1)
R = matrix('r', 1, 1) # буковка значит, что этот параметр мы оцениваем при помощи ММП.
Q = matrix(0, 1, 1)
x0 = matrix('a') # буковка значит, что этот параметр мы оцениваем при помощи ММП.
model_lt <- MARSS(y, model = list(Z = Z, B = B, A = A, U = U, R = R, Q = Q, x0 = x0)) # Модель локального уровняSuccess! abstol and log-log tests passed at 20 iterations.
Alert: conv.test.slope.tol is 0.5.
Test with smaller values (<0.1) to ensure convergence.
MARSS fit is
Estimation method: kem
Convergence test: conv.test.slope.tol = 0.5, abstol = 0.001
Estimation converged in 20 iterations.
Log-likelihood: -645.0764
AIC: 1296.153 AICc: 1296.324
Estimate
R.r 455.560
U.u -0.374
x0.a 101.212
Initial states (x0) defined at t=0
Standard errors have not been calculated.
Use MARSSparamCIs to compute CIs and bias estimates.states <- model_lt$states %>% c() # Извлекаем из модели результат - состояния
# Сделаем иллюстрацию:
tibble(Date = as.Date(data$Date),
Long_Run_state = states,
Urals = data$Urals) %>%
ggplot(aes(x = Date)) +
geom_point(aes(y = Urals), color = 'orange', alpha = 0.5) +
geom_line(aes(y = Long_Run_state), color = 'purple', size = 1.1, alpha = 0.4) +
theme_minimal(base_family = 'Merriweather') +
theme(plot.title = element_text(hjust = 0.5)) +
labs(title = 'Самая простая модель')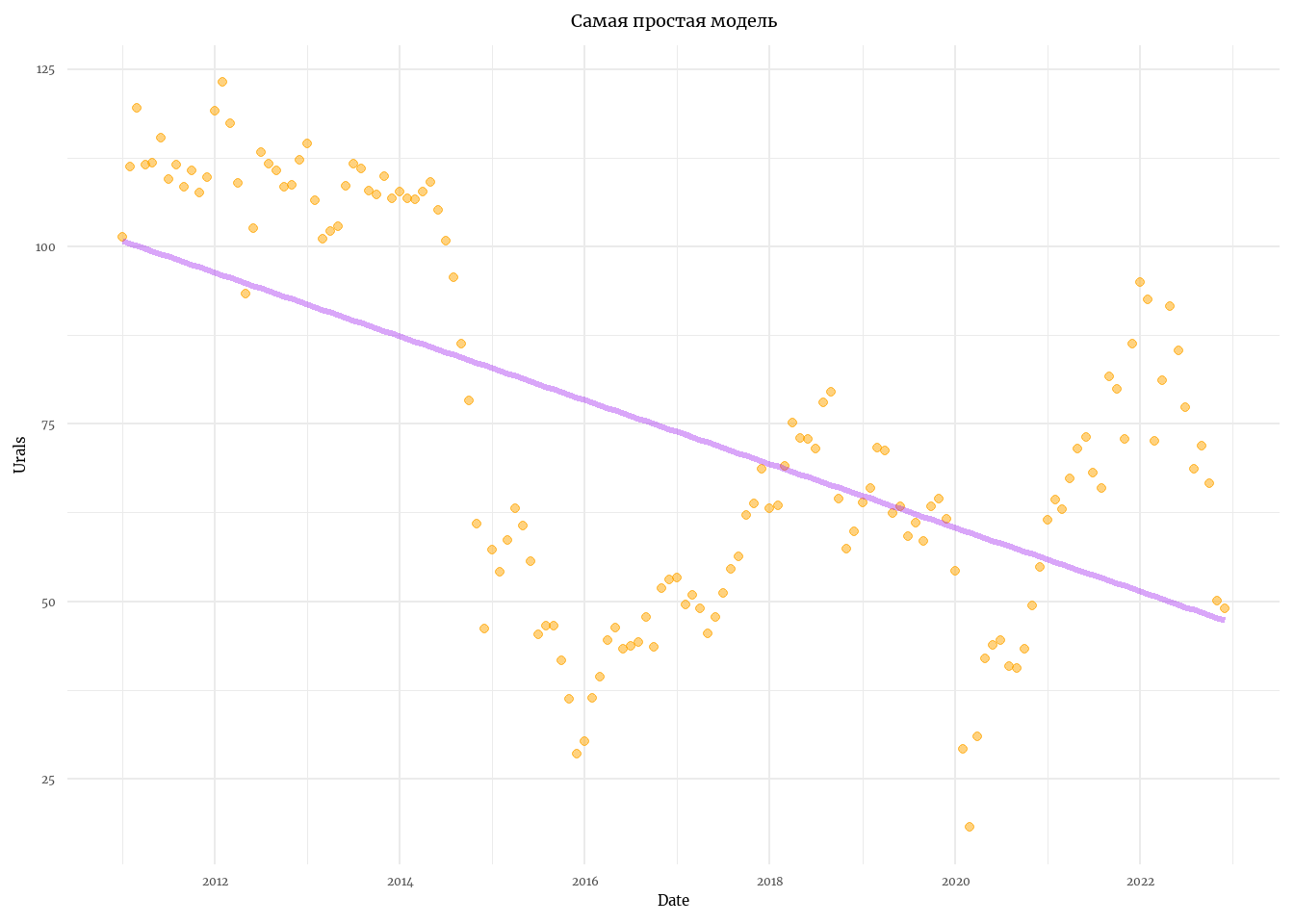
Стохастические состояния
Теперь мы переходим к более продвинутому пониманию тренда, как случайной величины. Мы исключаем из уравнения состояния компнненту, связанную с линейным трендом, \(u\), но прибавляем к каждому состоянию случайный, нормально распределённый шум, w. Вы могли узнать в этой модели случайное блуждание - это оно и есть.
Случайное блуждание - модель случайного процесса, в котором каждое последующее наблюдение равно сумме предыдущего наблюдения и нормального шума.
\[ \begin{align} &x_t = x_{t-1} + w_t, \space \space w_t \sim \mathcal{N}(0,q) \\ &y_t = x_t + v_t, \space \space v_t \sim \mathcal{N}(0,r) \\ &x_0 = a \end{align} \]
# Параметры
Z = matrix(1, 1, 1)
B = matrix(1, 1, 1)
A = matrix(0, 1, 1)
U = matrix(0, 1, 1) # Изменение здесь, теперь u не оценивается и равно 0.
R = matrix('r', 1, 1)
Q = matrix('q', 1, 1) # Дисперсия случайного шума.
x0 = matrix('a')
model_st_1 <- MARSS(y, model = list(Z = Z, B = B, A = A, U = U, R = R, Q = Q, x0 = x0)) # Модель локального уровняWarning! Abstol convergence only. Maxit (=500) reached before log-log convergence.
MARSS fit is
Estimation method: kem
Convergence test: conv.test.slope.tol = 0.5, abstol = 0.001
WARNING: Abstol convergence only no log-log convergence.
maxit (=500) reached before log-log convergence.
The likelihood and params might not be at the ML values.
Try setting control$maxit higher.
Log-likelihood: -475.2997
AIC: 956.5995 AICc: 956.7709
Estimate
R.r 0.192
Q.q 42.802
x0.a 101.401
Initial states (x0) defined at t=0
Standard errors have not been calculated.
Use MARSSparamCIs to compute CIs and bias estimates.
Convergence warnings
Warning: the R.r parameter value has not converged.
Type MARSSinfo("convergence") for more info on this warning.Success! abstol and log-log tests passed at 17 iterations.
Alert: conv.test.slope.tol is 0.5.
Test with smaller values (<0.1) to ensure convergence.
MARSS fit is
Estimation method: kem
Convergence test: conv.test.slope.tol = 0.5, abstol = 0.001
Estimation converged in 17 iterations.
Log-likelihood: -482.6861
AIC: 969.3722 AICc: 969.4573
Estimate
Q.q 35
x0.a 103
Initial states (x0) defined at t=0
Standard errors have not been calculated.
Use MARSSparamCIs to compute CIs and bias estimates.states_2 <- model_st_2$states %>% c() # Извлекаем из модели результат - состояния
# Сделаем иллюстрацию:
# Первый случай - overfitting
p1 <- tibble(Date = as.Date(data$Date),
State = states_1,
Urals = data$Urals) %>%
ggplot(aes(x = Date)) +
geom_point(aes(y = Urals), color = 'orange', alpha = 0.5) +
geom_line(aes(y = State), color = 'purple', size = 1.1, alpha = 0.4) +
theme_minimal(base_family = 'Merriweather') +
theme(plot.title = element_text(hjust = 0.5)) +
labs(title = 'Модель стохастического тренда, overfitting')
# Второй случай - r < q.
p2 <- tibble(Date = as.Date(data$Date),
State = states_2,
Urals = data$Urals) %>%
ggplot(aes(x = Date)) +
geom_point(aes(y = Urals), color = 'orange', alpha = 0.5) +
geom_line(aes(y = State), color = 'purple', size = 1.1, alpha = 0.4) +
theme_minimal(base_family = 'Merriweather') +
theme(plot.title = element_text(hjust = 0.5)) +
labs(title = 'Модель стохастического тренда, r < q')
p1 / p2 # Комбинируем графики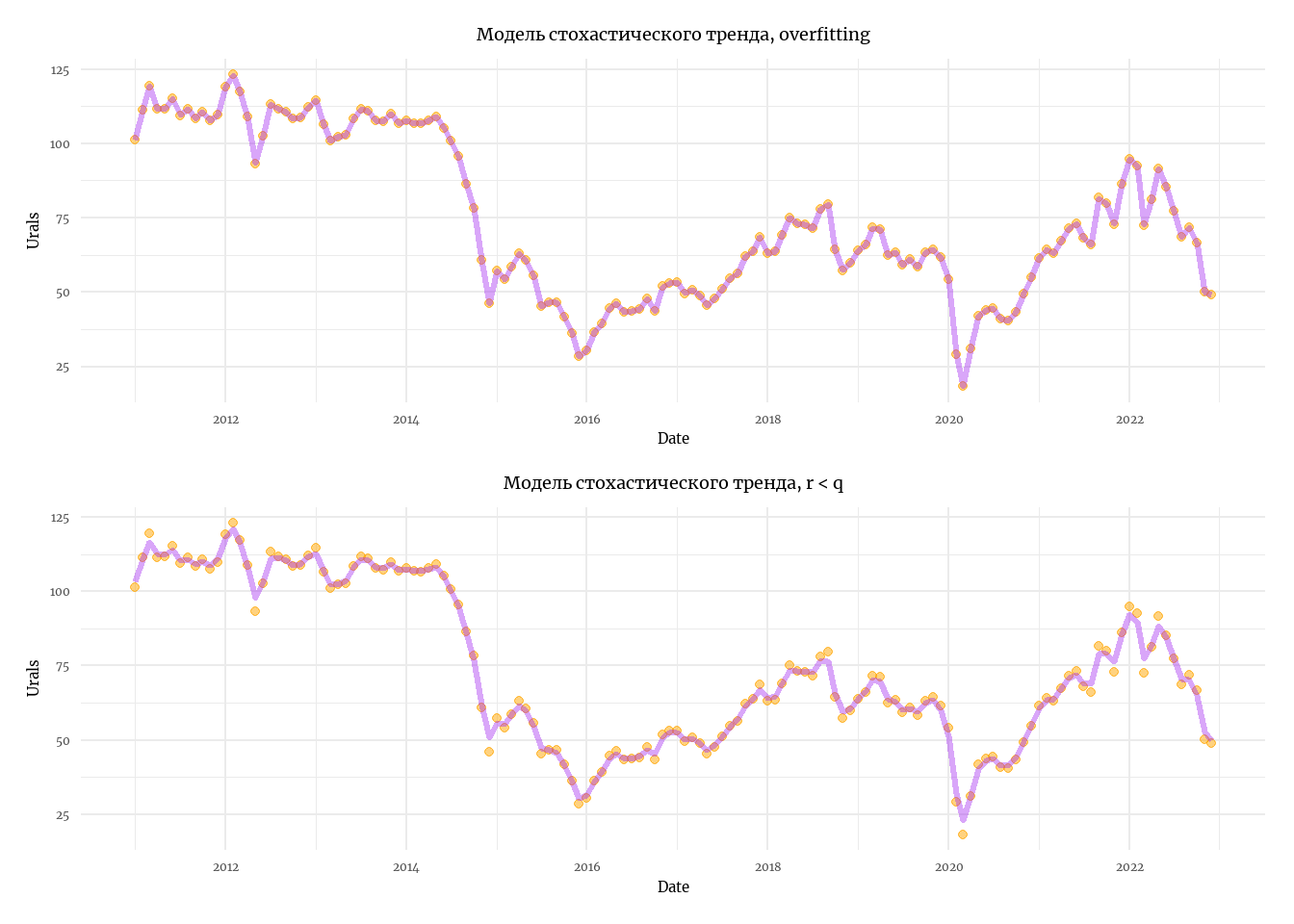
Меняющийся тренд
предположим, что тренд со временем может меняться. В прошлых задачах изменение тренда, состояния, определялось случайной величиной \(w_t\). Теперь мы хотим внести больше ясности в то, как устроено изменение тренда и моделируем ещё переменную состояния \(u_t\), которая влияет на \(x\), но не влияет напрямую на \(y\).
\[ \begin{align} &x_t = x_{t-1} + u_{t-1} + w_t, \space \space w_t \sim \mathcal{N}(0,q) \\ &u_t = u_{t-1} + z_t \space \space z_t \sim \mathcal{N}(0,p) \\ &y_t = x_t + v_t, \space \space v_t \sim \mathcal{N}(0,r) \\ &x_0 = a \end{align} \]
По мере углубления в модели пространства состояний нам всё больше будет требоваться линейная алгебра. Поскольку переменных состояний теперь 2, нам будет удобнее всё выписать в форме матриц:
\[ \begin{align} &x_t = Bx_{t-1} + u + w_t \\ &y_t = Zx + a + v_t, \space \space a = 0 \\ \end{align} \] И в совсем матричном виде:
\[ \begin{align} &\pmatrix{x_t \\ u_t} = \pmatrix{1 & 1 \\ 0 & 1}\pmatrix{x_{t-1} \\ u_{t-1}} + \pmatrix{v_t \\ z_t} , \space \space \pmatrix{v_t \\ z_t } \sim \mathcal{MVN}\left[\pmatrix{0\\0}, \pmatrix{q & 0 \\ 0 &p}\right] \\ &y_t = \pmatrix{1 & 0} \pmatrix{x_t \\ u_t} + 0 +\mathcal{N}(0, r) \end{align} \] Давайте запрограммируем эту модель:
Z = matrix(c(1,0), 1, 2)
B = matrix(c(1, 0, 1, 1), 2, 2)
A = matrix(0)
U = matrix(0, 2, 1)
R = matrix('r')
Q = matrix(c('q', 0, 0, 'p'), 2, 2)
x0 = matrix(c('x', 'u'), 2, 1)
model_ct <- MARSS(y, model = list(Z = Z, B = B, A = A, U = U, R = R, Q = Q, x0 = x0),
inits = list(x0 = matrix(c(74, -0.1), 2, 1)),
control = list(maxit = 20)
) # Модель меняющегося трендаWarning! Reached maxit before parameters converged. Maxit was 20.
neither abstol nor log-log convergence tests were passed.
MARSS fit is
Estimation method: kem
Convergence test: conv.test.slope.tol = 0.5, abstol = 0.001
WARNING: maxit reached at 20 iter before convergence.
Neither abstol nor log-log convergence test were passed.
The likelihood and params are not at the MLE values.
Try setting control$maxit higher.
Log-likelihood: -485.9664
AIC: 983.9328 AICc: 984.546
Estimate
R.r 4.91
Q.q 23.28
Q.0 -5.66
Q.p 3.61
x0.x 99.07
x0.u 3.27
Initial states (x0) defined at t=0
Standard errors have not been calculated.
Use MARSSparamCIs to compute CIs and bias estimates.
Convergence warnings
Warning: the R.r parameter value has not converged.
Warning: the logLik parameter value has not converged.
Type MARSSinfo("convergence") for more info on this warning.states_1 <- model_ct$states[1,] # Состояние x
states_2 <- model_ct$states[2,] # Состояние u
p1 <- tibble(Date = as.Date(data$Date),
State = states_1,
Urals = data$Urals) %>%
ggplot(aes(x = Date)) +
geom_point(aes(y = Urals), color = 'orange', alpha = 0.5) +
geom_line(aes(y = State), color = 'purple', size = 1.1, alpha = 0.4) +
theme_minimal(base_family = 'Merriweather') +
theme(plot.title = element_text(hjust = 0.5)) +
labs(title = 'Меняющийся тренд, x')
p2 <- tibble(Date = as.Date(data$Date),
State = states_2,
Urals = data$Urals) %>%
ggplot(aes(x = Date)) +
geom_line(aes(y = State), color = 'purple', size = 1.1, alpha = 0.4) +
theme_minimal(base_family = 'Merriweather') +
theme(plot.title = element_text(hjust = 0.5)) +
labs(title = 'Меняющийся тренд, u')
p1 / p2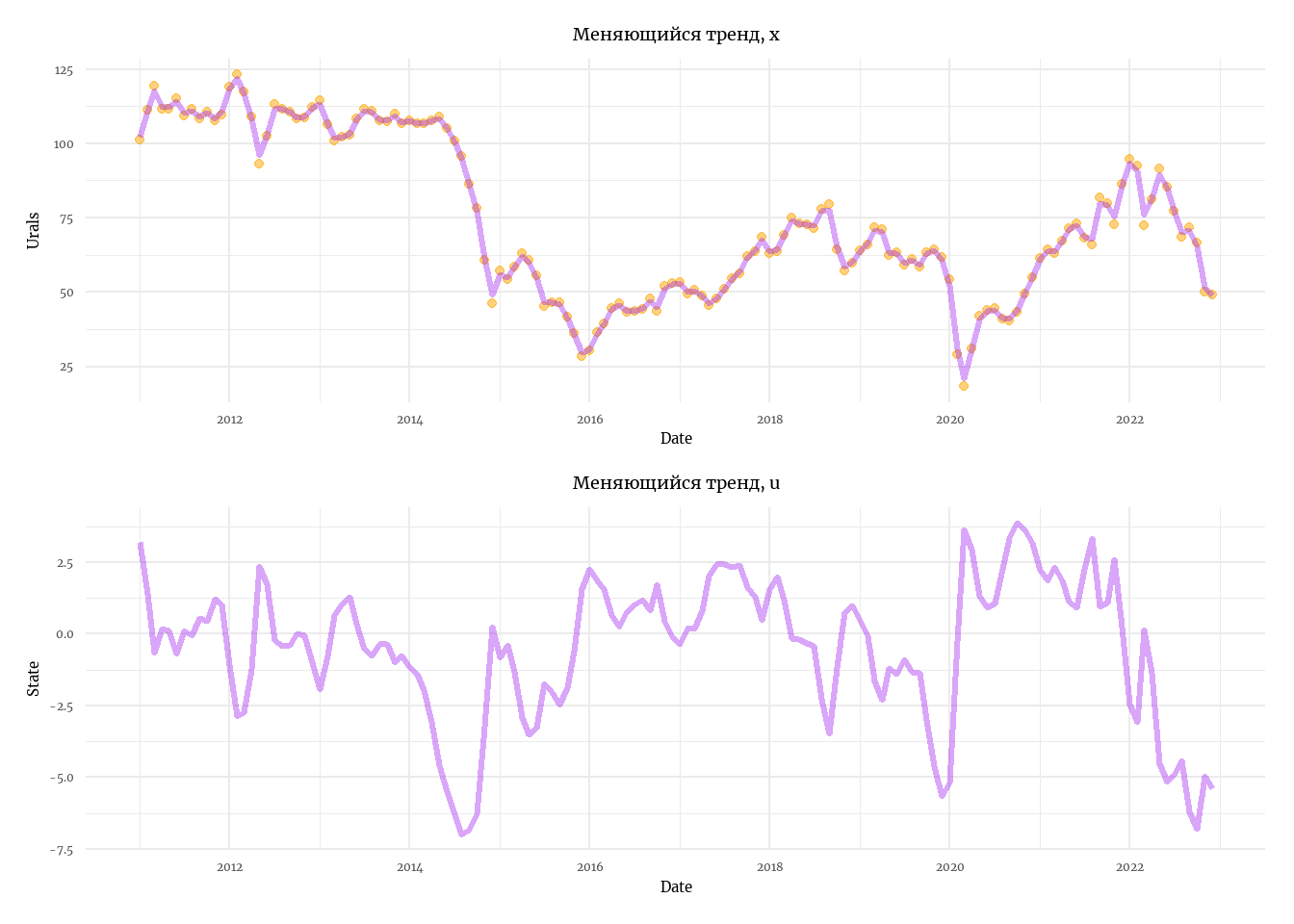
Как мы видим, такая модель может очень хорошо описывать исходные данные. Тем не менее, если мы хотим получить менее шумную информацию о тренде, мы можем уточнить некоторые параметры в модели, оставим для оценки только \(r\) - условную дисперсию исходных данных (условием в данном случае выступают прочие параметры, которые мы задали извне):
Z = matrix(c(1,0), 1, 2)
B = matrix(c(1, 0, 1, 1), 2, 2)
A = matrix(0)
U = matrix(0, 2, 1)
R = matrix('r')
Q = matrix(c(0.1, 0, 0, 0.1), 2, 2) # вместо q и p подставим малые значения
x0 = matrix(c(115, 0.1), 2, 1) # новые начальные условия
model_ct <- MARSS(y, model = list(Z = Z, B = B, A = A, U = U, R = R, Q = Q, x0 = x0),
control = list(maxit = 20)
) # Модель меняющегося трендаSuccess! algorithm run for 15 iterations. abstol and log-log tests passed.
Alert: conv.test.slope.tol is 0.5.
Test with smaller values (<0.1) to ensure convergence.
MARSS fit is
Estimation method: kem
Convergence test: conv.test.slope.tol = 0.5, abstol = 0.001
Algorithm ran 15 (=minit) iterations and convergence was reached.
Log-likelihood: -538.415
AIC: 1078.83 AICc: 1078.858
Estimate
R.r 56.8
Initial states (x0) defined at t=0
Standard errors have not been calculated.
Use MARSSparamCIs to compute CIs and bias estimates.states_1 <- model_ct$states[1,] # состояние x
states_2 <- model_ct$states[2,] # состояние u
resid <- (y - model_ct$states[1,]) %>% c()
p1 <- tibble(Date = as.Date(data$Date),
State = states_1,
Urals = data$Urals) %>%
ggplot(aes(x = Date)) +
geom_point(aes(y = Urals), color = 'orange', alpha = 0.5) +
geom_line(aes(y = State), color = 'purple', size = 1.1, alpha = 0.4) +
theme_minimal(base_family = 'Merriweather') +
theme(plot.title = element_text(hjust = 0.5)) +
labs(title = 'Меняющийся тренд, x')
p2 <- tibble(Date = as.Date(data$Date),
State = states_2,
Urals = data$Urals) %>%
ggplot(aes(x = Date)) +
geom_line(aes(y = State), color = 'purple', size = 1.1, alpha = 0.4) +
theme_minimal(base_family = 'Merriweather') +
theme(plot.title = element_text(hjust = 0.5)) +
labs(title = 'Меняющийся тренд, u')
p3 <- tibble(Date = as.Date(data$Date),
Residuals = resid,
Urals = data$Urals) %>%
ggplot(aes(x = Date)) +
geom_line(aes(y = Residuals), color = 'purple', size = 1.1, alpha = 0.4) +
theme_minimal(base_family = 'Merriweather') +
theme(plot.title = element_text(hjust = 0.5)) +
labs(title = 'Остатки (краткосрочная компонента)')
p1 / p2 / p3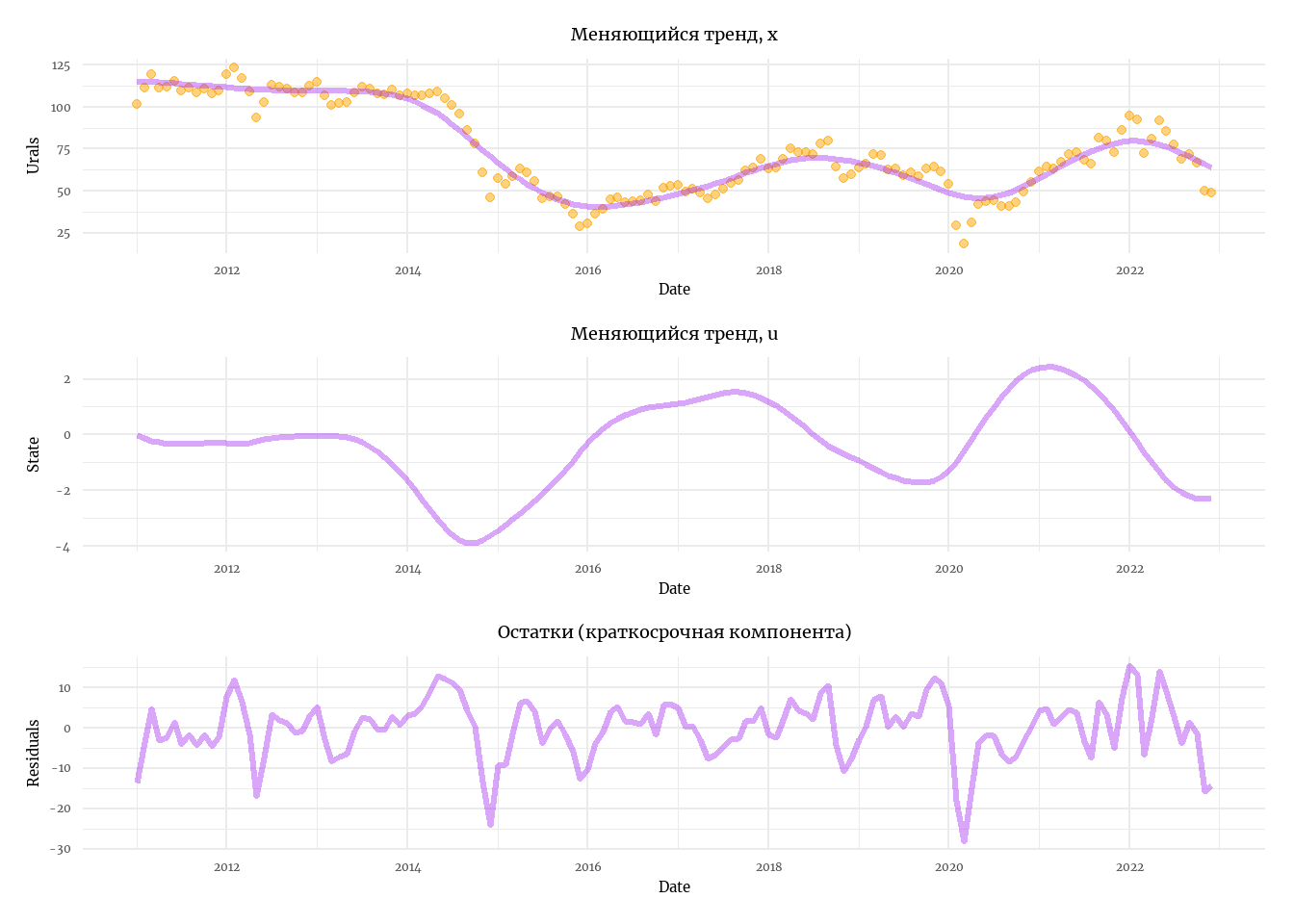
Теперь мы получили более гладкий тренд. Модели трендов, основанные на похожих идеях - фильтр Ходрика-Прескотта и фильтр Гамильона - современные методы выделения тренда из шумных данных. В большей степени сегодня используется последний.
Упражнение Попробуйте написать в
MARSSмодель фильтра Ходрика-Прескотта, на основе её описания в статье. Этот и многие другие фильтры уже выполнены в других библиотеках в R. Попробуйте функциюhpfilterиз библиотекиmFilter. Также в этой библиотеке есть фильтр Кристиано-Фицджеральда, Баттерворта и другие - вам не нужно выписывать всю модель пространства состояний, чтобы их использовать.
Пример:
Мы научились выделять из шумных данных линейный меняющийся тренд. Теперь поговорим о сезонности!
Сезонность
Зачастую, когда мы смотрим на графики переменных, подверженных сильной сезонности, мы не понимаем, в каком состоянии находится временной ряд. Представьте, каково эконометрической модели, пытающейся оценить причинно-следственные связи в таких шумных данных! Проблемы сезонности также решаются при помощи моделей пространства состояний. Для этого нам потребуется ввести в модель экзогенные переменные.
data_s <- data$Output %>%
t() # Возьмём наиболее подверженный сезонности ряд из нашего датасета - выпуск
period <- 12
per.lst <- 1
TT <- 144
# Месяцы, как факторные переменные:
c.in <- diag(period)
for (i in 2:(ceiling(TT / period))){
c.in <- cbind(c.in, diag(period))
}
c.in <- c.in[, (1:TT) + (per.lst -1)]
rownames(c.in) <- month.abb
# Модель в терминах библиотеки MARSS
B <- 'diagonal and unequal' # диагональная матрица, в которой элементы по диагонали - разные параметры
Q <- 'diagonal and unequal'
U <- 'zero' # нулевая матрица.
Z <- 'identity' # I
A <- 'zero'
R <- 'diagonal and unequal'
D <- 'zero'
d <- 'zero'
C <- 'unconstrained' # матрица, все элементы которой - параметры.
model.list <- list(B = B, Q = Q, U = U, Z = Z, A = A, R = R, D = D, d = d, C = C, c = c.in)
seas_1 <- MARSS(data_s, model = model.list,
control = list(maxit = 1500)) # Получим месячные поправочные коэффициентыWarning! Abstol convergence only. Maxit (=1500) reached before log-log convergence.
MARSS fit is
Estimation method: kem
Convergence test: conv.test.slope.tol = 0.5, abstol = 0.001
WARNING: Abstol convergence only no log-log convergence.
maxit (=1500) reached before log-log convergence.
The likelihood and params might not be at the ML values.
Try setting control$maxit higher.
Log-likelihood: -1017.972
AIC: 2067.944 AICc: 2072.227
Estimate
R.R 49.71
B.B 0.97
Q.Q 80829.82
x0.x0 20578.13
C.(X.Y1,Jan) -1775.45
C.(X.Y1,Feb) -577.48
C.(X.Y1,Mar) 459.27
C.(X.Y1,Apr) 1527.65
C.(X.Y1,May) 1318.62
C.(X.Y1,Jun) 1102.60
C.(X.Y1,Jul) 879.58
C.(X.Y1,Aug) 1242.41
C.(X.Y1,Sep) 1615.73
C.(X.Y1,Oct) 1999.55
C.(X.Y1,Nov) 847.85
C.(X.Y1,Dec) -338.96
Initial states (x0) defined at t=0
Standard errors have not been calculated.
Use MARSSparamCIs to compute CIs and bias estimates.
Convergence warnings
Warning: the R.R parameter value has not converged.
Type MARSSinfo("convergence") for more info on this warning.Если мы пытаемся очистить данные от сезонности, то сезонная компонента должна прибавляться к данным, а не к состоянию. Напишем модель “наоборот”:
# Модель
B <- 'identity'
Q <- 'diagonal and unequal'
U <- matrix('u')
Z <- 'diagonal and unequal'
A <- 'zero'
R <- 'diagonal and unequal'
D <- 'unconstrained'
d <- c.in
C <- 'zero'
c <- 'zero'
model.list <- list(B = B, Q = Q, U = U, Z = Z, A = A, R = R, D = D, d = c.in, C = C, c = c)
seas_2 <- MARSS(data_s, model = model.list,
control = list(maxit = 1500))Warning! Reached maxit before parameters converged. Maxit was 1500.
neither abstol nor log-log convergence tests were passed.
MARSS fit is
Estimation method: kem
Convergence test: conv.test.slope.tol = 0.5, abstol = 0.001
WARNING: maxit reached at 1500 iter before convergence.
Neither abstol nor log-log convergence test were passed.
The likelihood and params are not at the MLE values.
Try setting control$maxit higher.
Log-likelihood: -1028.386
AIC: 2090.772 AICc: 2095.629
Estimate
Z.Z 0.998
R.R 51.985
U.u 45.403
Q.Q 93774.125
x0.x0 19126.691
D.(Y1,Jan) -940.846
D.(Y1,Feb) -2034.393
D.(Y1,Mar) -2105.656
D.(Y1,Apr) -1178.310
D.(Y1,May) -565.415
D.(Y1,Jun) -250.901
D.(Y1,Jul) -203.144
D.(Y1,Aug) 209.866
D.(Y1,Sep) 1025.122
D.(Y1,Oct) 2267.981
D.(Y1,Nov) 2399.111
D.(Y1,Dec) 1404.092
Initial states (x0) defined at t=0
Standard errors have not been calculated.
Use MARSSparamCIs to compute CIs and bias estimates.
Convergence warnings
Warning: the R.R parameter value has not converged.
Warning: the logLik parameter value has not converged.
Type MARSSinfo("convergence") for more info on this warning.Model used in SEATS is different: (1 1 2)(0 1 1)plotting_df %>%
ggplot(aes(x = date)) +
geom_line(aes(y = Output), color = 'orange', alpha = 0.3, size = 1.2) + # Данные
geom_line(aes(y = states_1), color = 'pink', alpha = 0.9, size = 1.4) + # Наша простая модель
geom_line(aes(y = seas_1), color = 'green', alpha = 0.4, size = 1.4) + # X13
theme_minimal(base_family = 'Merriweather') +
labs(title = 'Убираем сезонность в данных',
subtitle = 'Пример - выпуск',
x = '', y = '')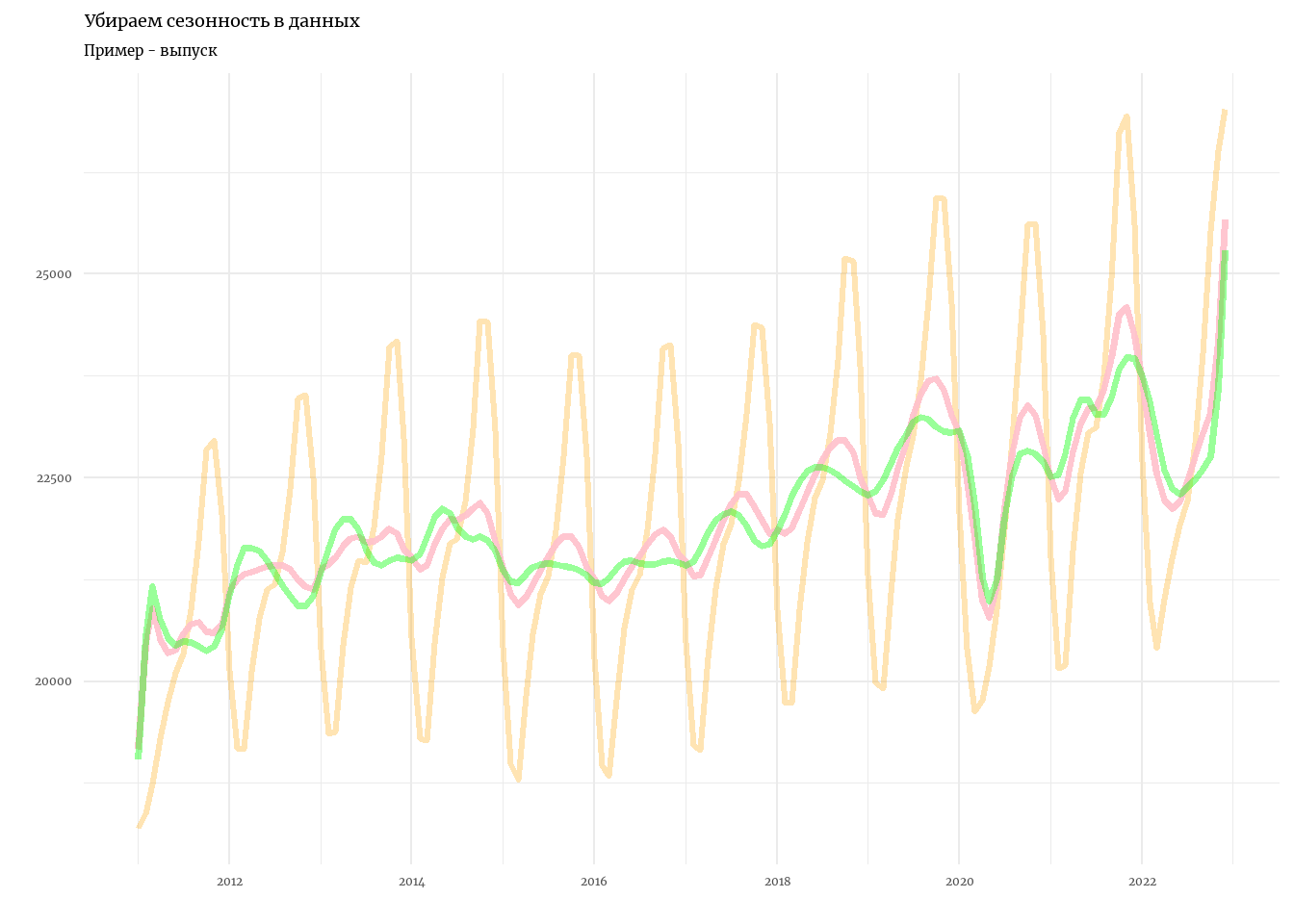
Второй алгоритм - X13 - самый популярный сегодня для работы с сезонностью. Он работает почти так же, как тот, который мы запрограммировали тут, его также можно реализовать и адаптировать в MARSS для любых интересных нам рядов. Но лучше всего использовать специальные библиотеки, где он уже реализован. например - seasonal.
Также прошу заметить, что в нашем результате как будто есть сезонность. Она происходит оттого, что ряд по ВВП - не исходные данные Росстата, а дезагрегированные данные до месячных.
Многомерные случаи и экзогенные переменные
Давайте смоделируем следующую систему уравнений:
\[ \begin{align} &\pmatrix{\pi_t \\ y_t} = \pmatrix{a_1 \\ a_2} + \pmatrix{\beta_{\pi,er} & \beta_{\pi,urals} \\ \beta_{y,er} & \beta_{y, urals}} \pmatrix{er_{t-1} \\ urals_{t-1}} + \pmatrix{v_\pi \\ v_{er}} \end{align} \]
data_mv <- tibble(
dcpi = diff(log(data$CPI)),
dout = diff(log(data$Output))
) %>%
t() # логдифференциалы для эндогенных переменных
data_exog <- tibble(
dusd = diff(log(data$USD)),
durals = diff(log(data$Urals))
) %>%
t() # логдифференциалы для экзогенных переменных
Q <- matrix(c('qpi', 0, 0, 'qo'), 2, 2) # ковариация между выпуском и ценами равна 0
U <- 'zero' # отсутствие трендов в состояниях
x0 <- matrix(c('pi0', 'y0'), 2, 1) # начальные условия
B <- 'identity' # Отсутствие связи между выпуском и инфляцией
Z <- 'identity'
d <- data_exog # Экзогенные переменные
A <- 'zero' # Отсутствие тренда в данных
D <- matrix(c('b1', 'b2', 'b3', 'b4'), 2, 2) # Параметры влияния экзогенных переменных на данные
model_mv <- MARSS(data_mv, model = list(B = B, U = U, Q = Q, Z = Z, A = A,
D = D, d = d, x0 = x0),
) # модельSuccess! abstol and log-log tests passed at 477 iterations.
Alert: conv.test.slope.tol is 0.5.
Test with smaller values (<0.1) to ensure convergence.
Alert: Numerical warnings were generated. Print the $errors element of output to see the warnings.
MARSS fit is
Estimation method: kem
Convergence test: conv.test.slope.tol = 0.5, abstol = 0.001
Estimation converged in 477 iterations.
Log-likelihood: 797.5484
AIC: -1575.097 AICc: -1574.297
Estimate
R.diag 3.20e-05
Q.qpi 5.86e-08
Q.0 8.69e-06
Q.qo 1.46e-03
x0.pi0 -8.90e-04
x0.y0 9.16e-03
D.b1 9.81e-02
D.b2 -7.85e-02
D.b3 2.60e-03
D.b4 -1.45e-02
Initial states (x0) defined at t=0
Standard errors have not been calculated.
Use MARSSparamCIs to compute CIs and bias estimates.
MARSSkem warnings. Type MARSSinfo() for help.
60919 warnings. First 10 shown. Type cat(object$errors) to see the full list.
iter=51 Setting element of R to 0, blocked. See MARSSinfo("R0blocked"). The error is due to the following MARSSkemcheck errors.
MARSSkemcheck error: t=1: For method=kem (EM), if an element of the diagonal of R is 0, the corresponding row of both A and D must be fixed. See MARSSinfo('AZR0').
iter=51 Setting element of R to 0, blocked. See MARSSinfo("R0blocked"). The error is due to the following MARSSkemcheck errors.
MARSSkemcheck error: t=2: For method=kem (EM), if an element of the diagonal of R is 0, the corresponding row of both A and D must be fixed. See MARSSinfo('AZR0').
iter=51 Setting element of R to 0, blocked. See MARSSinfo("R0blocked"). The error is due to the following MARSSkemcheck errors.
MARSSkemcheck error: t=3: For method=kem (EM), if an element of the diagonal of R is 0, the corresponding row of both A and D must be fixed. See MARSSinfo('AZR0').
iter=51 Setting element of R to 0, blocked. See MARSSinfo("R0blocked"). The error is due to the following MARSSkemcheck errors.
MARSSkemcheck error: t=4: For method=kem (EM), if an element of the diagonal of R is 0, the corresponding row of both A and D must be fixed. See MARSSinfo('AZR0').
iter=51 Setting element of R to 0, blocked. See MARSSinfo("R0blocked"). The error is due to the following MARSSkemcheck errors.
MARSSkemcheck error: t=5: For method=kem (EM), if an element of the diagonal of R is 0, the corresponding row of both A and D must be fixed. See MARSSinfo('AZR0').
iter=51 Setting element of R to 0, blocked. See MARSSinfo("R0blocked"). The error is due to the following MARSSkemcheck errors.
MARSSkemcheck error: t=6: For method=kem (EM), if an element of the diagonal of R is 0, the corresponding row of both A and D must be fixed. See MARSSinfo('AZR0').
iter=51 Setting element of R to 0, blocked. See MARSSinfo("R0blocked"). The error is due to the following MARSSkemcheck errors.
MARSSkemcheck error: t=7: For method=kem (EM), if an element of the diagonal of R is 0, the corresponding row of both A and D must be fixed. See MARSSinfo('AZR0').
iter=51 Setting element of R to 0, blocked. See MARSSinfo("R0blocked"). The error is due to the following MARSSkemcheck errors.
MARSSkemcheck error: t=8: For method=kem (EM), if an element of the diagonal of R is 0, the corresponding row of both A and D must be fixed. See MARSSinfo('AZR0').
iter=51 Setting element of R to 0, blocked. See MARSSinfo("R0blocked"). The error is due to the following MARSSkemcheck errors.
MARSSkemcheck error: t=9: For method=kem (EM), if an element of the diagonal of R is 0, the corresponding row of both A and D must be fixed. See MARSSinfo('AZR0').
iter=51 Setting element of R to 0, blocked. See MARSSinfo("R0blocked"). The error is due to the following MARSSkemcheck errors.
MARSSkemcheck error: t=10: For method=kem (EM), if an element of the diagonal of R is 0, the corresponding row of both A and D must be fixed. See MARSSinfo('AZR0').cpi_fit <- MARSSkf(model_mv)$xtT[1,] # состояния
out_fit <- MARSSkf(model_mv)$xtT[2,]
p1 <- tibble(date = as.Date(data$Date[2:nrow(data)]),
CPI = diff(log(data$CPI)),
Output = data$Output %>% log %>% diff,
CPI_fit = cpi_fit,
Output_fit = out_fit) %>%
ggplot(aes(x = date)) +
geom_point(aes(y = CPI)) +
geom_line(aes(y = cpi_fit)) +
theme_bw() +
labs(title = 'Инфляция') # график модели для инфляции
p2 <- tibble(date = as.Date(data$Date[2:nrow(data)]),
CPI = diff(log(data$CPI)),
Output = data$Output %>% log %>% diff,
CPI_fit = cpi_fit,
Output_fit = out_fit) %>%
ggplot(aes(x = date)) +
geom_point(aes(y = Output)) +
geom_line(aes(y = Output_fit)) +
theme_bw() +
labs(title = 'Выпуск')
p1 / p2 # patchwork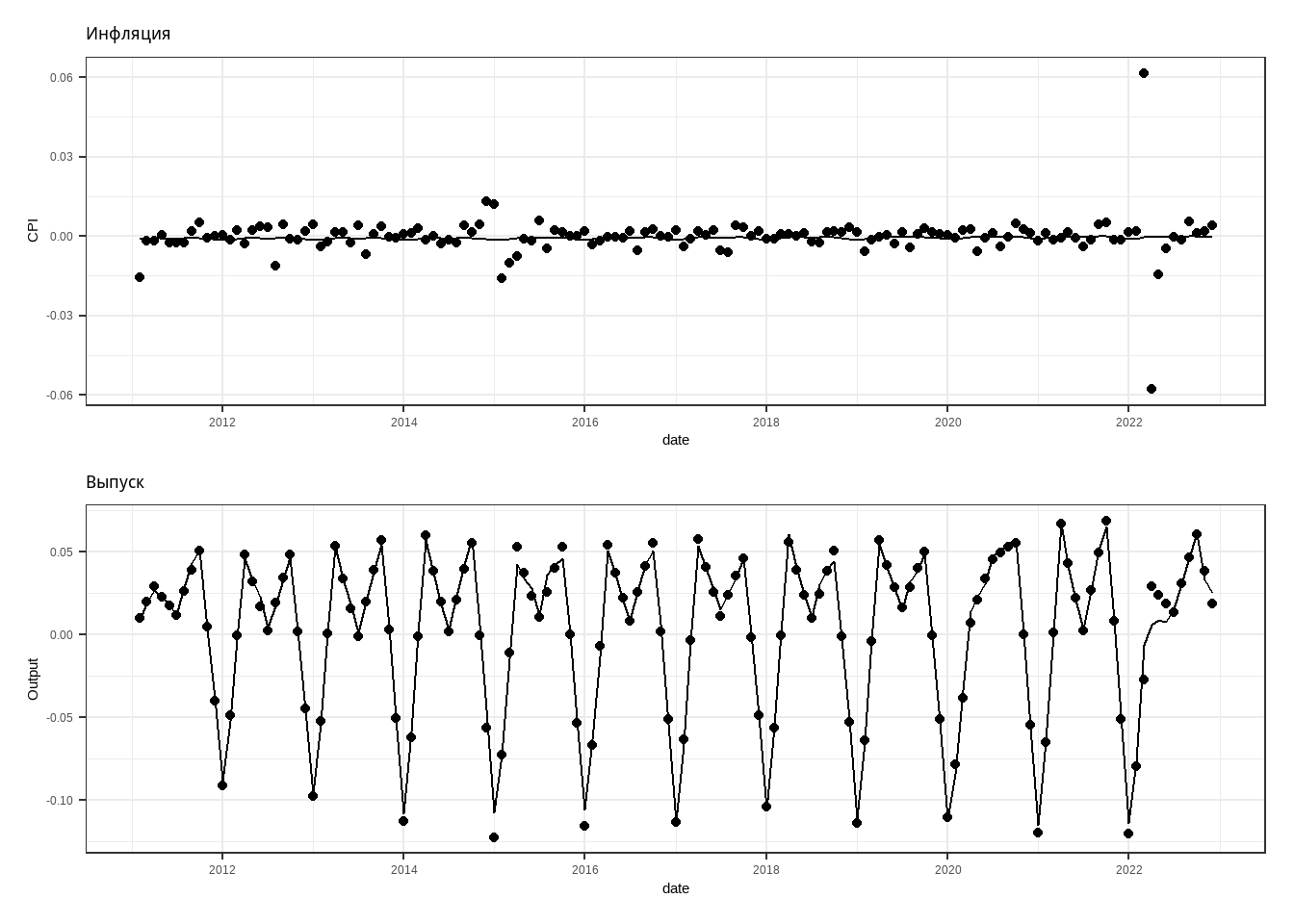
Заполнение пропусков в данных прии помощи фильтра Калмана
Частным случаем прогнозирования является заполнение пропусков в данных. Для временных рядов отлично подходит фильтр Калмана. В этом примере мы возьмём данные о курсе рубля и случайным образом уберём 60 наблюдений из имеющихся у нас 144. Притворимся на время, что их нет. Затем построим три простых модели пространства состояний:
- Случайное блуждание.
\[ \begin{align} &x_t = x_{t-1} + w_t, \space \space w_t \sim \mathcal{N}(0, q) \\ &y_t = x_t + v_t, \space \space w_t \sim \mathcal{N}(0, r) \\ &x_0 = a \end{align} \]
- Случайное блуждание с трендом.
\[ \begin{align} &x_t = x_{t-1} + u + w_t, \space \space w_t \sim \mathcal{N}(0, q) \\ &y_t = x_t + v_t, \space \space w_t \sim \mathcal{N}(0, r) \\ &x_0 = a \end{align} \]
- Модель с трендом и экзогенной инфляцией.
\[ \begin{align} &x_t = x_{t-1} + u + C\pi_{t} + w_t, \space \space w_t \sim \mathcal{N}(0, q) \\ &y_t = x_t + v_t, \space \space w_t \sim \mathcal{N}(0, r) \\ &x_0 = a \end{align} \]
Предполагается, что чем более совершенна наша модель, тем лучше она заполняет пропуски в данных.
# Данные о валютном курсе
er_na <- data %>%
select(USD) %>%
t()
sample_nas <- sample(1:length(er_na), 60, replace = F) # выбираем случайным образом 60 значений от 1 до 144 без повторений.
er_na[sample_nas] <- NA # Создаём на месте этих номеров пропуски.
# Инфляция для модели с экзогенной инфляциенй
cpi <- data %>%
select(CPI) %>%
t()
cpi <- cpi - 100
# Одномерный фильтр без тренда (случайное блуждание)
B <- matrix(1)
Z <- matrix(1)
Q <- matrix('q')
U <- matrix(0)
A <- matrix(0)
R <- matrix('r')
model_1 <- MARSS(er_na, model = list(U = U, A = A, B = B, Z = Z, Q = Q, R = R),
control = list(maxit = 2000))Success! abstol and log-log tests passed at 35 iterations.
Alert: conv.test.slope.tol is 0.5.
Test with smaller values (<0.1) to ensure convergence.
MARSS fit is
Estimation method: kem
Convergence test: conv.test.slope.tol = 0.5, abstol = 0.001
Estimation converged in 35 iterations.
Log-likelihood: -274.2454
AIC: 554.4907 AICc: 554.7907
Estimate
R.r 10.0
Q.q 14.5
x0.x0 28.1
Initial states (x0) defined at t=0
Standard errors have not been calculated.
Use MARSSparamCIs to compute CIs and bias estimates.Success! abstol and log-log tests passed at 35 iterations.
Alert: conv.test.slope.tol is 0.5.
Test with smaller values (<0.1) to ensure convergence.
MARSS fit is
Estimation method: kem
Convergence test: conv.test.slope.tol = 0.5, abstol = 0.001
Estimation converged in 35 iterations.
Log-likelihood: -273.895
AIC: 555.79 AICc: 556.2963
Estimate
R.r 10.220
U.u 0.265
Q.q 14.078
x0.x0 26.925
Initial states (x0) defined at t=0
Standard errors have not been calculated.
Use MARSSparamCIs to compute CIs and bias estimates.Success! abstol and log-log tests passed at 17 iterations.
Alert: conv.test.slope.tol is 0.5.
Test with smaller values (<0.1) to ensure convergence.
MARSS fit is
Estimation method: kem
Convergence test: conv.test.slope.tol = 0.5, abstol = 0.001
Estimation converged in 17 iterations.
Log-likelihood: -262.7943
AIC: 535.5886 AICc: 536.3578
Estimate
R.r 5.99
U.u -1.08
Q.q 12.81
x0.x0 21.86
C.c 2.46
Initial states (x0) defined at t=0
Standard errors have not been calculated.
Use MARSSparamCIs to compute CIs and bias estimates.# Сделаем иллюстрацию
final <- tibble(date = data$Date %>% as.Date(),
er_na = er_na %>% c(),
er = data$USD,
model_1 = MARSSkf(model_1)$xtT %>% c(),
model_2 = MARSSkf(model_2)$xtT %>% c(),
model_3 = MARSSkf(model_3)$xtT %>% c()
)
final %>%
pivot_longer(model_1:model_3) %>%
ggplot(aes(x = date)) +
geom_point(aes(y = er_na), size = 1.4, color = 'grey40', alpha = 0.5) +
geom_line(aes(y = value, color = name), size = 1.1, alpha = 0.7, show.legend = F) +
rcartocolor::scale_color_carto_d(palette = 'TealRose') +
facet_wrap(~name, nrow = 3) +
theme_bw(base_family = 'Merriweather') +
labs(y = 'Обменный курс',
x = '')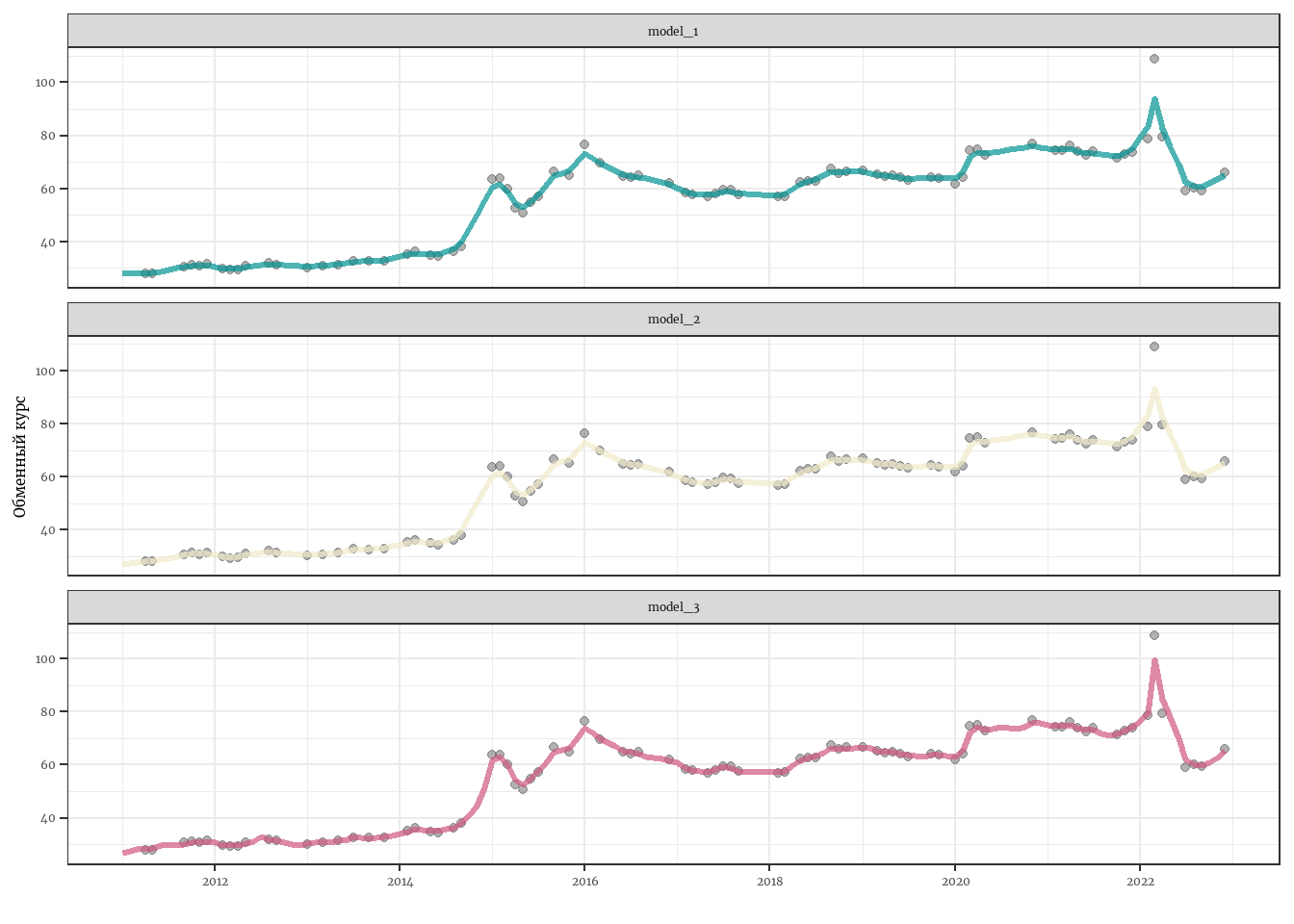
Сравним средние ошибки в заполнении пропусков для каждой модели:
final[sample_nas,] %>% # выбираем только те строки, в которых мы ранее создали пустые значения
mutate(error_1 = (er - model_1)^2, # столбцы с квадратами ошибок
error_2 = (er - model_2)^2,
error_3 = (er - model_3)^2
) %>%
filter(date != '2022-03-01') %>% # убираем наблюдение за март 2022 года.
summarize(across(c(error_1, error_2, error_3), base::sum),
.groups = 'drop') %>% # сумма по каждому столбцу
sqrt() / 60 # Средняя ошибка для одного наблюдения error_1 error_2 error_3
1 0.366446 0.3706022 0.3989415Ура, фильтр Калмана работает! Действительно, чем больше факторов мы учитывали, тем точнее былаташа модель.
Сегодня мы научились
- Понимать, как устроены модели пространства состояний и способ оценки состояний - фильтр Калмана.
- Строить модели тренда.
- Убирать сезонность из данных.
- Строить многомерные модели причинно-следственных связей.
Следующие шаги и полезные приложения:
- Дезагрегирование. Например, у вас есть какая-то модель все переменные в которой доступны вам на месячном уровне. Все, кроме одной, для которой вы имеете только квартальные значения. С помощью подходящей модели пространства состояний вы модете преобразовать этот квартальный ряд в месячный без сильной потери информативности. Особенно здорово - если у вас есть рефернесный ряд на месячном уровне, который описывает примерно то же самое, что интересующий ряд, требующий дезагрегирования.
- Nowcast. Предположим, у вас есть какая-то модель с данными. Все данные в модели публикуются примерно в одно время. Все, кроме одного ряда, который запаздывает на месяц другой. При помощи модели пространства состояний вы можете сделать оценку текущего состояния для данного ряда при наличии референсных рядов.
- Обновление методики расчёта показателей. Допустим, вы Росстат. Вы публикуете индексы цен на различные товары, например - смартфон. Год от года смартфоны, на основе которых рассчитывается индекс - разные. Поэтому вам нужно обновлять индекс роста цен на смартфоны каким-то более продуманным способом, чем просто соединять ряды: индекс цен = Nokia N73 до 2008 г, Потом Айфон 3, потом… Делать так плохо и неправильно. Лучше всего - использовать динамическую факторную модель (DFM) - частный случай моделей пространства состояний, который вы тоже можете реализовать в MARSS или в какой-нибудь другой библиотеке.
- Прочие приложения, связанные с прогнозированием, заполнением пропуском в данных временных рядов.