Парадокс Монти Холла в R

Автор

Е. Тымченко

Дата публикации

18 апреля 2023 г.

Сегодня мы положим начало серии статей про статистическое программирование и разберём ~~один баян~~ парадокс Монти Холла. Вот, как его пересказывает Википедия:

Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трёх дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, номер 3, за которой находится коза. После этого он спрашивает вас — не желаете ли вы изменить свой выбор и выбрать дверь номер 2? Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор? Также известно, что: * автомобиль равновероятно размещён за любой из трёх дверей; * ведущий знает, где находится автомобиль; * ведущий в любом случае обязан открыть дверь с козой (но не ту, которую выбрал игрок) и предложить игроку изменить выбор; * если у ведущего есть выбор, какую из двух дверей открыть (то есть, игрок указал на верную дверь, и за обеими оставшимися дверями — козы), он выбирает любую из них с одинаковой вероятностью.

В такой постановке задачи, участник может выбрать:

Решение 1 - Не менять выбор двери.
Решение 2 - Изменить выбор после того. как ведущий открыл одну из дверей

Если участник угадал, он получает машину!

Решим задачу аналитически

Предположим, участник изначально выбрал дверь 1. Обозначим события:

\(A_i\) - приз за дверью \(i\)

\(B_i\) - ведущий откроет дверь \(i\)

\[\mathbb{P}(A_1|B_2) = \mathbb{P}(B_2|A_1)\mathbb{P}(A_1)/\mathbb{P}(B_2) = \frac{1/2 \times 1/3}{1/2} = 1/3\]

\[\mathbb{P}(A_3|B_2) = \mathbb{P}(B_2|A_3)\mathbb{P}(A_3)/\mathbb{P}(B_2) = \frac{1 \times 1/3}{1/2}=2/3\]

Теперь запрограммируем эту задачу

Загрузим библиотеки, чтобы позже нарисовать красивую картинку:

library(tidyverse) # основная библиотека для обработки данных и построения графиков
library(hrbrthemes) # темы для графиков
library(sysfonts) # биллиотека для работы с шрифтами
library(showtext) # для компиляции шрифтов в ggplot
library(rcartocolor) # для работы с цветом
showtext_auto() 

font_add_google('Monoton') # импорт красивого шрифта из googlefonts

Эта функция симулирует одинарноее участие в данной лотерее при двух возможных значениях переменной SwitchPolicy - \(\{True, False\}\).

MontyHall <- function(SwitchPolicy){
  prize <- sample(1:3, 1) # Приз за случайной из дверей 1-3.
  choice <- sample(1:3, 1) # Участник выбирает одну из дверей.
  if(prize == choice){ # если выбор участника совпал с дверью, за которой лежит приз
    revealed <- setdiff(1:3, choice) %>% # ведущий открывает одну из оставшихся двух дверей.
      sample(1)
  }else{ # Если же участник изначально выбрал дверь, за которой была коза,
    revealed <- setdiff(1:3, c(prize, choice)) # ведущий открывает другую дверь с козой.
  }
  
  if(SwitchPolicy){ # Если участник True = передумал
  choice <- setdiff(1:3, c(revealed, choice))[1] # То его окончательный выбор - это не та дверь,
  } # которую открыл ведущий, и не та, которую он выбрал изначально.
  return(choice == prize) # Покажи нам только, угадал ли участник дверь с призом за ней (True или False).
}

Теперь мы можем вычислить искомую вероятность выигрыша при выборе Switch симулировав N лотерей.

WinProb <- function(Switch, N){
wins <- c()
for (i in 1:N){
   wins[i]<- MontyHall(Switch)
}
wins %>% 
  mean() %>%
  return()
}

Можно поиграть этими функциями, посмотреть, что всё работает:

MontyHall(T)

[1] TRUE

WinProb(F, 1000)

[1] 0.34

WinProb(T, 1000)

[1] 0.651

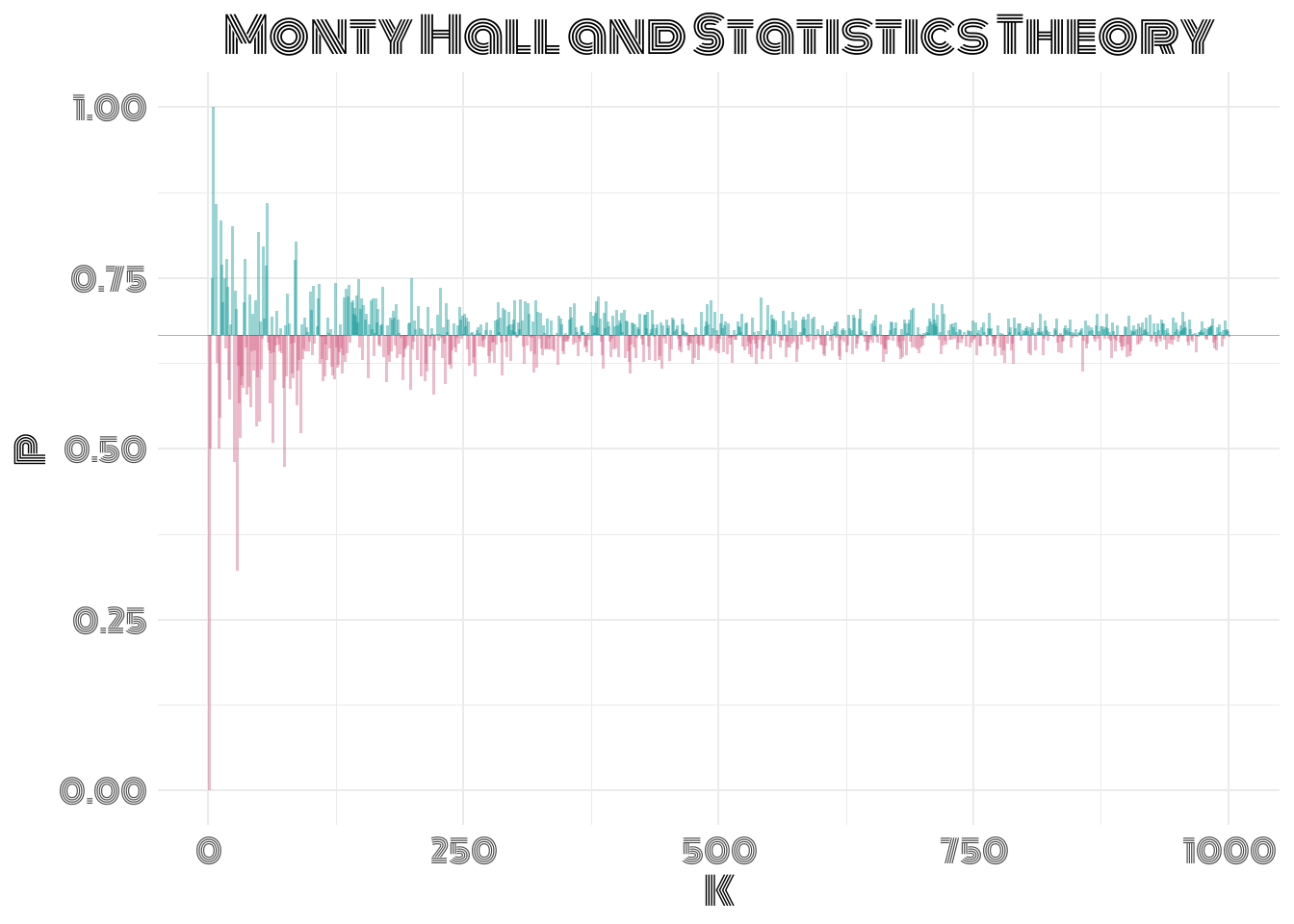
Теперь нарисуем, как вероятность выигрыша при смене выбора сходится к своему истинному значению при увеличении числа испытаний. Действительно, для проверки статистических гипотез часто требуется большая выборка:

set.seed(123)
K = 1000
WinProb_K <- c()
for (j in 1:K){
  WinProb_K[j] <- WinProb(T, j)
}

data.frame(P = WinProb_K,
           K = seq(1, K, by = 1)) %>%
  mutate(mycolor = ifelse(P > 0.66667, "type1", "type2")) %>%
  ggplot(aes(x = K, y = P)) +
  geom_segment(aes(x = K, xend = K, y = 0.66667, yend = P, color = mycolor), size = 0.7, alpha = 0.4, show.legend = F) +
  geom_hline(yintercept = 0.66667, size = 0.2, alpha = 0.3)  +
  scale_color_carto_d(palette = 'TealRose') +
  theme_minimal(base_family = 'Monoton') +
  theme(plot.title = element_text(hjust = 0.5, size = 38),
        axis.title.x= element_text(size = 30),
        axis.title.y = element_text(size = 30),
        axis.text.x = element_text(size = 25),
        axis.text.y = element_text(size = 25),
        plot.background = element_rect(colour = 'white')
        ) +
  labs(title = 'Monty Hall and Statistics Theory')